thousandsaints
- 2
- 0
I really need help understanding this problem. I'd be really thankful if someone could explain it to me.
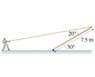
A man is attempting to raise a 7.5 m long, 29 kg flagpole that has a hinge at the base by pulling on a rope attached to the top of the pole. The figure of the problem is below as an attachment
With what force does the man have to pull on the rope to hold the pole motionless in this position?
\tau=F*r\bot
Net torque = 0
I tried finding the torque caused the weight of the flagpole, and then the torque caused by the man. From that I tried finding the force which the man exerts. But I can't find the correct answer.
Torque from gravity = w*r\bot =mg*Lcos(\Theta) =(9.81*29)*7.5cos30 = 1848 Nm
Torque from the man = F*r\bot = F*Ltan\Theta = F*7.5tan20 = F*2.73m
The two torque values should equal each other. so...
1848 Nm = F*2.73m
F= 1848 Nm / 2.73
F= 676.8 N
Homework Statement
A man is attempting to raise a 7.5 m long, 29 kg flagpole that has a hinge at the base by pulling on a rope attached to the top of the pole. The figure of the problem is below as an attachment
With what force does the man have to pull on the rope to hold the pole motionless in this position?
Homework Equations
\tau=F*r\bot
Net torque = 0
The Attempt at a Solution
I tried finding the torque caused the weight of the flagpole, and then the torque caused by the man. From that I tried finding the force which the man exerts. But I can't find the correct answer.
Torque from gravity = w*r\bot =mg*Lcos(\Theta) =(9.81*29)*7.5cos30 = 1848 Nm
Torque from the man = F*r\bot = F*Ltan\Theta = F*7.5tan20 = F*2.73m
The two torque values should equal each other. so...
1848 Nm = F*2.73m
F= 1848 Nm / 2.73
F= 676.8 N
Attachments
Last edited: