friscoboya
- 6
- 1
Hello
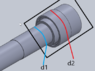
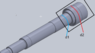
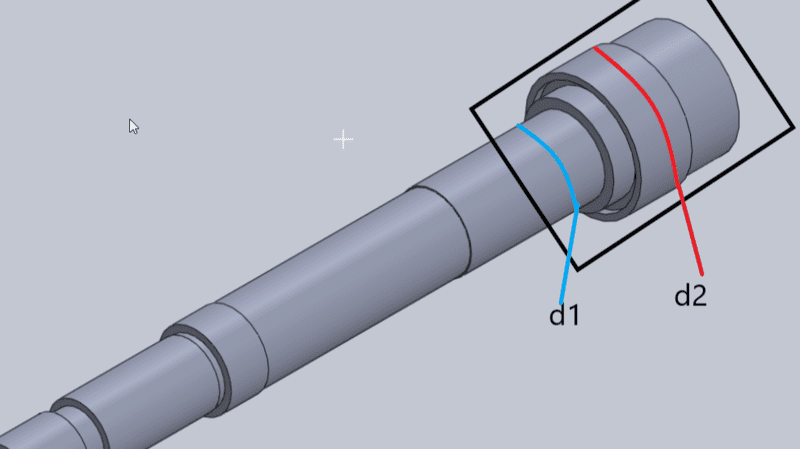
I am doing a shaft design layout for a spindle to minimize deflection and I have to calculate the area moment of inertia for a shaft overhang.The shaft overhang is the distance from a bearing to the end of the shaft. Here is a picture detailing the location of the overhang. The black square would be the shaft overhang. Would I calculate the area moment of inertia for d1 and d2, add them together and average them? Or what is the correct method to add area moment of inertias? The equation for hollow cylinder area moment of inertia is.
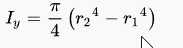
Thanks
I am doing a shaft design layout for a spindle to minimize deflection and I have to calculate the area moment of inertia for a shaft overhang.The shaft overhang is the distance from a bearing to the end of the shaft. Here is a picture detailing the location of the overhang. The black square would be the shaft overhang. Would I calculate the area moment of inertia for d1 and d2, add them together and average them? Or what is the correct method to add area moment of inertias? The equation for hollow cylinder area moment of inertia is.
Thanks