How to Calculate Center of Pressure (hf) for a Tank?

[knoxox_]

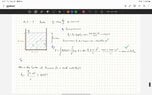
Homework Statement

I'm trying to fully understand the calculation of, the center of pressure (hf), for a vertical tank wall with a fluid of uniform density. The pressure distribution is linear, starting from zero at the surface and increasing to ρgh at the bottom.

Specifically, I would like to understand:
-The general derivation of the center of pressure hf

Relevant Equations

I’m aware of the formula hf=(∫h⋅dF)/F Where F is the resultant force on the wall of the tank.

 

[haruspex]

The idea of the centre of pressure is that it is the point where a single supporting force on one side of a lamina would balance the total force from the fluid on the other side.
So the net torque from the fluid about that point is zero.
If its height is c then $\int F(y).(y-c).dy=0$.