How to Calculate <Ly^2> Without Using Symmetry?

[physics1000]

Hi, I have a question.
Let us say we have the wave function as with eigen value and base eigen value of:
$!\psi >\:=\:\frac{1}{6}\left(4!1,0,0>\:+\:3!2,1,1>\:-1!2,1,0\:+\:\sqrt{10}!2,1,-1>\right)$
I need to find <Ly^2>
the solution of the problem according to answers, is demanding that <Lx^2>=<Ly^2> ( Due to symmetry ) which I have no idea why.
If I dont want to use that symmetry ( let us say I did not know that at the test ), how do I calculate it?
I tried calculating it using formulas, it is impossible...

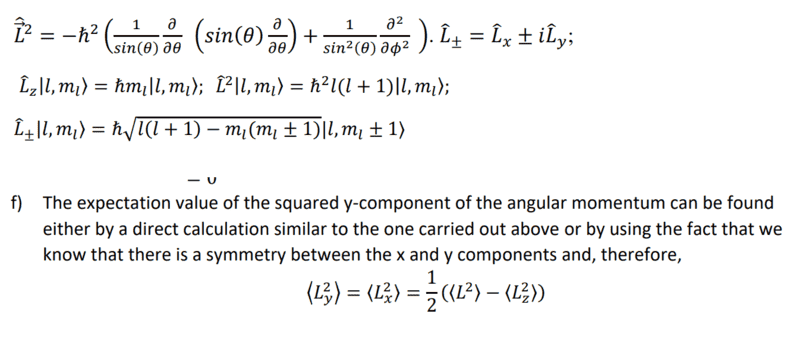
The beginning is from our formulas, f) is the solution.
How do I find it without saying <Ly^2>=<Lx^2>? ( finding <L^2> and <Lz^2> is easy )
Edit:
Of course it is easy also to find lx and ly using lower and upper operators, but doing square, is impossible...

 

[vanhees71]

Can you write your formula in readable form, using LaTeX? Here's the LaTeX Guide (the link is directly under the input form):

https://www.physicsforums.com/help/latexhelp/

Of course, you can apply
$$\hat{L}_x=\frac{1}{2}(\hat{L}_+ + \hat{L}_-)$$
twice to the state ket to get what $\hat{L}_x^2$ does on the state. Analogously it works for $\hat{L}_y^2$.

 

[physics1000]

Can you write your formula in readable form, using LaTeX? Here's the LaTeX Guide (the link is directly under the input form):

https://www.physicsforums.com/help/latexhelp/

Of course, you can apply
$$\hat{L}_x=\frac{1}{2}(\hat{L}_+ + \hat{L}_-)$$
twice to the state ket to get what $\hat{L}_x^2$ does on the state. Analogously it works for $\hat{L}_y^2$.

Hi, thanks for the answer, but sadly it doesn't answer :(
I will try to fix, it may take time.
about what you said.
I said I tried with operator above and below, it will not work.
you may try, but you see, there are calculations that with sqrt and such... ( I thought of it, as said in the edit ).
That is why I asked for another way to reach it if possible :\
If there is, I will just remember the symmetry ( although I have no idea why it is true )

 

[physics1000]

Why cant I edit the original post?
I want to write it, but I cant edit it.

EDIT:
You can close thread.
If i need to put my answer from before question and write it here, it will take me a few hours and the test is really soon.
Thanks anyway for trying to help :)

 

[Old Person]

Hi.

My best guess is that the formula should have looked like this:

$\vert\psi >\:=\:\frac{1}{6}\left(4|1,0,0>\:+\:3|2,1,1>\:-1|2,1,0>\:+\:\sqrt{10}|2,1,-1>\right)$

That's a state vector written in ket notation = a superposition of eigenstates labelled with what look like principal quantum numbers.

@physics1000 you can right-click on any LaTeX formula in any post and choose to see how that was encoded as LaTeX. The above was done just using \vert to create a vertical line and/or taking the character | straight from my keyboard.

Why cant I edit the original post?

I think this forum has a policy that discourages that. Users can only edit a post for about an hour after they first posted it. If there's an important reason for editing after that you have to seek assistance from a moderator. There's some fair reasons for this, e.g. existing replies may be left looking odd or irrelevant. I am NOT staff, I don't know, that's my best knowledge and belief.

the solution of the problem according to answers, is demanding that <Lx^2>=<Ly^2> ( Due to symmetry ) which I have no idea why.

I haven't seen the full details of the original question but from what you have shown, the question really should be "why wouldn't that symmetry be there?"
You have some information that specifies an m quantum number so that would tie down the z-axis a little. However you are free to orientate the x and y axis as you wish and the information in the question would be unaffected. Maintaining a left-handed convention for the axis, you could choose to rotate around the z-axis so that the x axis becomes the y-axis and the new y-axis becomes negative (points the other way to) the old x-axis. Under that symmetry you must have
(x-axis angular momentum components) = - (components in the y-axis) .

Computing the expectation values of SQUARES of $L_x$ and $L_y$ you can ignore the sign change.

NOTE: I'm not an expert. Advice is offered only to the best of my ability. My motivation: People helped me with a question recently, seems fair to try and pass that help on.
Good luck with the test etc.

 

[vanhees71]

Well, but what's wrong with calculating how the "ladder operators" act on this state? It's not that difficult!

 

[Old Person]

@vanhees71, I agree. From what the OP has shown of the model answers, it is clearly stated that you can solve the problem in many ways.