How to calculate self energy Feynman diagram like that

[Safinaz]

Hi all ,

I try to calculate the squared amplitude of the following self energy digram :

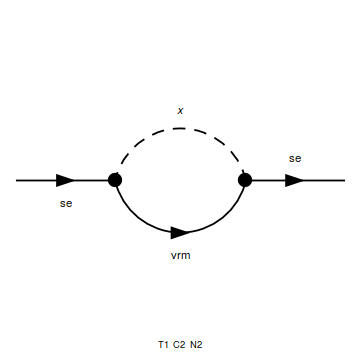where se is massless Dirac fermion , and vrm is massless right handed neutrino. x is a scalar with mass m ..

I wrote the nominator of this process as:

N = $\bar{u}(p) (1-\gamma_5) (p\!\!\!/ +k\!\!\!/ ) (1+\gamma_5) u(p) \to p\!\!\!/ (1-\gamma_5) (p\!\!\!/ +k\!\!\!/ ) (1+\gamma_5) \to p\!\!\!/ (1-\gamma_5) (p\!\!\!/ +k\!\!\!/ ) \to p_\alpha \gamma^\alpha (1-\gamma_5) (p_\alpha \gamma^\alpha + k_\beta \gamma^\beta ) \to p_\alpha p_\alpha \gamma^\alpha \gamma^\alpha +p_\alpha k_\beta\gamma^\alpha \gamma^\beta - p_\alpha \gamma^\alpha \gamma_5 p_\alpha \gamma^\alpha - p_\alpha \gamma^\alpha \gamma_5 k_\beta \gamma^\beta$

I don't know how the first term as $p_\alpha p_\alpha \gamma^\alpha \gamma^\alpha$ can be calculated or the third term .. also I don't know how $P.K$ which comes from the second term can be calculated from the process kinematics ? while $P^2 =0$ and $K^2 = m_\chi^2$

Note that: the momentums of the particles in the Feynman diagram are se(p), vrm(p+k) and x(k)

Also the "x se vrm " vertices come from these Lagrangian terms:

$y (\bar{\nu_R^c} \chi s + \bar{s} \chi \nu_R^c )$ (where s-> se, $\chi$ -> x and \nu -> vrm)

Thanks ..

 

[Dr.AbeNikIanEdL]

For the terms you asked for: Wikipedia has a useful list of identities: https://en.wikipedia.org/wiki/Gamma_matrices#Feynman_slash_notation. I am not sure if I follow your steps though. Are there traces implied over your terms? Also, $k^2 \neq m_\chi^2$, as $k^\mu$ is the loop momentum you are integrating over.

Edit: Also, for a self energy you would not necessarily write it between spinors, probably you could expand more on what you actually want to calculate...

 

[Safinaz]

Are there traces implied over your terms

Yes, sure .. I forgot Tr [] :(

Also, for a self energy you would not necessarily write it between spinors

Now it getting worse .. the nominator becomes:

$N = Tr [ (1-\gamma_5) (p\!\!\!/ +k\!\!\!/ ) (1+\gamma_5) \to (1-\gamma_5) (p\!\!\!/ +k\!\!\!/ ) ] \to 0$

since:

Trace of any product of an odd number of $\gamma^\mu$ is zero and trace of $\gamma^5$ times a product of an odd number of $\gamma^\mu$ is also zero ..

 

[ChrisVer]

Why do you write same indices more than once?

 

[Safinaz]

Which indices ? I think the veritecs and momentums are all clear in the question

 

[Dr.AbeNikIanEdL]

Now it getting worse ..

But you only have a trace if there are spinors. In this case all your terms just need traces (and I think you are missing a factor of two from $(1-\gamma_5)(1-\gamma_5) = 2(1-\gamma_5)$).

Which indices ?

For example

→$p_\alpha p_\alpha\gamma^\alpha\gamma^\alpha$

would be more readable as $p_\alpha p_\beta\gamma^\alpha\gamma^\beta$.

 

[vanhees71]

It's not only "more readable" but it's a meaningful expression. Each index can occur maximally twice, and in this case one must be an upper and one a lower index, and this implies by convention that you sum over this index from 0 to 3 (Einstein summation convention). If the same index occurs more than twice or two same upper or lower indices, than the expression is wrong.

 

[Safinaz]

But you only have a trace if there are spinors. In this case all your terms just need traces

Also, for a self energy you would not necessarily write it between spinors

So some thing is not clear now, do I write the spinors ? that is the right ?

and I think you are missing a factor of two

Yap .. but forget about numbers now, actually it will be a factor of 1/2, because $P_L = (1-\gamma^5)/2$ and $P_R = (1+\gamma^5)/2$

Why do you write same indices more than once?

I will say why .. please look the following Feynman digram of the process

I have in N $p\!\!\!/$ comes from the spinors and $p\!\!\!/$ appear in $(p\!\!\!/+k\!\!\!/)$ from the fermion propagtor, so it's the same momentum or p .. I wonder if it will be meaningfull if i used different indecis for like $p_\alpha \gamma^\alpha (1-\gamma_5) (p_\delta \gamma^\delta + k_\beta \gamma^\beta )$ ?

 

[Dr.AbeNikIanEdL]

So some thing is not clear now, do I write the spinors?

The self energy $\Sigma(p)$ is usually defined as just the 1PI blob, for which at lowest order your diagram would contribute. There are no spinors involved. You can of course write down the expression for $\bar{u}(p)\Sigma(p)u(p)$, but I am not aware what this expression would mean. What observable do you want to calculate?

I have in N p/p/ p\!\!\!/ comes from the spinors and p/p/ p\!\!\!/ appear in (p/+k/)(p/+k/) (p\!\!\!/+k\!\!\!/) from the fermion propagtor, so it's the same momentum or p .

That is why you call it $p$ both times. But the contracted indices mean summation e.g. $p_\alpha\gamma^\alpha = \sum_{\alpha=0}^3 p_\alpha\gamma^\alpha$. The sums in the two $\slash{p}$ expressions have their own indices.

I wonder if it will be meaningfull if i used different indecis for like pαγα(1−γ5)(pδγδ+kβγβ)pαγα(1−γ5)(pδγδ+kβγβ) p_\alpha \gamma^\alpha (1-\gamma_5) (p_\delta \gamma^\delta + k_\beta \gamma^\beta ) ?

That would be the expression.

 

[Safinaz]

So now "P.K" or $p_\mu k^\mu$ what does it equal ? 'd we use CMF kinematics here ? but I wonder how ..

 

[Dr.AbeNikIanEdL]

Well , $k^\mu$ is the loop momentum you are integrating over, so you need to calculate something like $p_\mu \int \frac{d^4k}{(2\pi)^4} \frac{k^\mu}{D}$, where $D$ means the denominator corresponding to your diagram.

 

[Safinaz]

but I am not aware what this expression would mean. What observable do you want to calculate?

I want to calculate the mass of a particle $s$ on the loop level ..

 

[Dr.AbeNikIanEdL]

so you indeed just need the self energy

 

[vanhees71]

What's you interaction? I can only guess from your a bit strange posting #1 that it might be the coupling
$$\mathcal{L}_{\text{int}}=g \overline{\psi} \mathrm{i} \gamma^5 \psi \phi,$$
where $\psi$ is a Dirac spinor and $\phi$ a (pseudo-)scalar field. The corresponding Feynman rule is that the three-point vertex is $-g \gamma^5$. The propagator lines are
$$G(p)=\frac{\gamma_{\mu} p^{\mu}+m}{p^2-m^2+\mathrm{i} 0^+}, \quad D(p)=\frac{1}{p^2-M^2+\mathrm{i} 0^+},$$
for the fermion and boson respectively.

Now apply the Feynman rules. The self-energy is truncated, i.e., the external legs are not considered. They just tell you that you have a self-energy. Now you have to read the diagram against the direction of the spinor legs. Then taking into account the symmetry factor you get
$$\sigma(p)=-g^2 \int \mathrm{d}^4 l \frac{1}{(2 \pi)^4} \gamma^5 \mathrm{i} G(l+p) \gamma^5 \mathrm{i} D(l).$$
Now you can use standard formulae (e.g., regularizing with dimensional regularization) and evaluate the diagram, which is linearly divergent, i.e., you need a wave-function and a mass counter term to make the diagram finite, as expected.