- #1
weningth
- 6
- 2
- TL;DR Summary
- An electron emits a photon. The amplitude for this process is calculated and then the polarisation sum for the photon is performed. However, the terms proportional to the unphysical polarisations do not vanish. Why is that?
Consider the process [itex]e^-\rightarrow e^-\gamma[/itex] depicted in the following Feynman diagram.
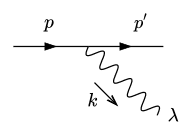
The spin-averaged amplitude with linearly polarised photons is
[tex]\overline{|M|^2}=8\pi\alpha\left(-g^{\mu\nu}+\epsilon^\mu_+\epsilon^\nu_-+\epsilon^\mu_-\epsilon^\nu_+\right)\left(p_\mu p^\prime_\nu+p_\nu p^\prime_\mu-g_{\mu\nu}pp^\prime\right),[/tex]
where the polarisation sum for massless vector bosons was used in terms of the unphysical polarisation vectors [itex]\epsilon_\pm=\frac{1}{\sqrt{2}}\left(\epsilon_t\pm\epsilon_L\right)[/itex], [itex]\epsilon_t=(1,\mathbf{0}), \epsilon_L=\frac{1}{|\mathbf{k}|}(0,\mathbf{k})[/itex].
Now, by the Ward identity the parts of the amplitude of the form [itex]\epsilon^\mu_\pm M_\mu[/itex] should vanish since [itex]\epsilon_+\parallel k[/itex]. However, since [itex]\epsilon_+\epsilon_-=1[/itex] I find that instead
$$\overline{|M|^2}=16\pi\alpha\left(\epsilon^\mu_+p\epsilon^\nu_-p^\prime+\epsilon^\mu_-p\epsilon^\nu_+p^\prime\right).$$
I know that in general the Ward identity does not hold for individual diagrams but only for the sum of all relevant ones. However, the above diagram is the only one to this order in [itex]\alpha[/itex].
Why does the term [itex]\left(\epsilon^\mu_+\epsilon^\nu_-+\epsilon^\mu_-\epsilon^\nu_+\right)\left(p_\mu p^\prime_\nu+p_\nu p^\prime_\mu-g_{\mu\nu}pp^\prime\right)[/itex] not vanish?
The spin-averaged amplitude with linearly polarised photons is
[tex]\overline{|M|^2}=8\pi\alpha\left(-g^{\mu\nu}+\epsilon^\mu_+\epsilon^\nu_-+\epsilon^\mu_-\epsilon^\nu_+\right)\left(p_\mu p^\prime_\nu+p_\nu p^\prime_\mu-g_{\mu\nu}pp^\prime\right),[/tex]
where the polarisation sum for massless vector bosons was used in terms of the unphysical polarisation vectors [itex]\epsilon_\pm=\frac{1}{\sqrt{2}}\left(\epsilon_t\pm\epsilon_L\right)[/itex], [itex]\epsilon_t=(1,\mathbf{0}), \epsilon_L=\frac{1}{|\mathbf{k}|}(0,\mathbf{k})[/itex].
Now, by the Ward identity the parts of the amplitude of the form [itex]\epsilon^\mu_\pm M_\mu[/itex] should vanish since [itex]\epsilon_+\parallel k[/itex]. However, since [itex]\epsilon_+\epsilon_-=1[/itex] I find that instead
$$\overline{|M|^2}=16\pi\alpha\left(\epsilon^\mu_+p\epsilon^\nu_-p^\prime+\epsilon^\mu_-p\epsilon^\nu_+p^\prime\right).$$
I know that in general the Ward identity does not hold for individual diagrams but only for the sum of all relevant ones. However, the above diagram is the only one to this order in [itex]\alpha[/itex].
Why does the term [itex]\left(\epsilon^\mu_+\epsilon^\nu_-+\epsilon^\mu_-\epsilon^\nu_+\right)\left(p_\mu p^\prime_\nu+p_\nu p^\prime_\mu-g_{\mu\nu}pp^\prime\right)[/itex] not vanish?