GreatEscapist
- 178
- 0
Homework Statement
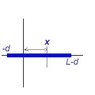
Calculate by direct integration the moment of inertia for a thin rod of mass M and length L about an axis located distance d from one end.
Homework Equations
I = Ʃmir2i
Which can be rewritten as int (r2)dm as Δm -> 0
Since we cannot integrate over a mass, we need to switch to dx, which is dm = M/L dx
The Attempt at a Solution
The question is asking us to find the moment of inertia as it rotates on an axis d from one end.
Normally, if we are trying to find the moment of inertia of an "infinitely thin" rod rotating on one end, the moment of inertia is (1/3)ML2
However, we have to manually integrate this problem because we have mass on both sides of the axis of rotation.
I took two integrals- one on one side of d, and on the other.
First side:
(M/d) int(x2)dx (with bounds 0 to d)
(M/d)(x3/3) (with bounds 0 to d)
= Md2/3
The second side:
(M/L-d) int(x2) dx (with bounds from d to L)
(M/L-d) (x3/3) (with bounds from d to L)
(M/L-d) ( (L3/3) - (d3/3))Then I added the two moments of inertia together, to get:
(Md2/3) + (M/L-d)((L3/3) - (d3/3))
This answer is not correct, and I was wondering where i went wrong conceptually/mathematically. Homework is due soon, so any immediate help is greatly appreciated.