SUMMARY
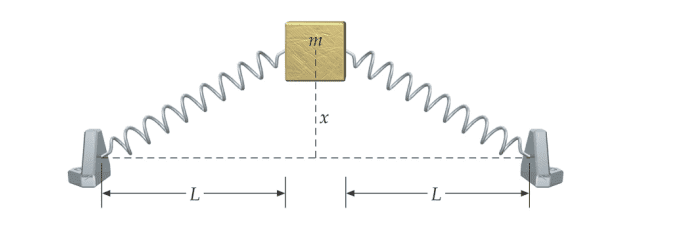
The discussion centers on calculating the potential energy (PE) of a spring-mass system. The correct formula for the potential energy is established as PE(x) = mgx + 1/2*k*(x/sin(a) - L)^2 + 1/2*k*(x/sin(a) - L)^2. Participants clarify that the gravitational potential energy (mgx) should be included only if the motion is vertical; otherwise, it should be omitted. The kinetic energy (KE) is defined as KE(x) = 1/2*m*(dx/dt)^2, emphasizing that the mass m is the only contributor to kinetic energy, not the springs.
PREREQUISITES
- Understanding of potential energy in mechanical systems
- Familiarity with Hooke's Law and spring constants (k)
- Knowledge of gravitational potential energy (mgx)
- Basic calculus for relating kinetic energy to velocity (dx/dt)
NEXT STEPS
- Study the derivation of potential energy in spring systems
- Learn about the principles of energy conservation in mechanical systems
- Explore the application of differential equations in motion analysis
- Investigate the effects of angle on spring force components
USEFUL FOR
Students studying physics, particularly those focusing on mechanics, engineers working with spring systems, and anyone interested in energy calculations in mechanical contexts.