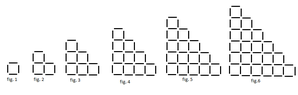marsman
- 2
- 0
Please help! I need to be able to find the number of total toothpicks used in any given figure in this sequence, in addition to total squares in any figure, using the figure number.View attachment 1592
The only way I can figure this out is by listing them all out one by one, which is TERRIBLE :(
Thank you so much in advance!
The only way I can figure this out is by listing them all out one by one, which is TERRIBLE :(
Thank you so much in advance!