How to convert a slope to an acceleration?

[Ellio]

Homework Statement

"From the slope (of the graphic) you calculated, determine the acceleration of the object."

Relevant Equations

Slope: Δy/Δx
Gravitational acceleration on Earth ≅ 9.81 m/s²

Hello, I hope you are all very well.
I am in second year of High School and I have a practical work in physics.
The experiment was to release a long tape with a mass of 40g at the end from a certain height. An instrument would hit the tape 50 times/s and put a mark each time. From that we have to complete a series of exercises.

One of the exercise is however causing me some trouble. We had to write down the different position of all the mark that are on the tape on a graphic. The first one is a x(t) graphic and the second one x(t²).
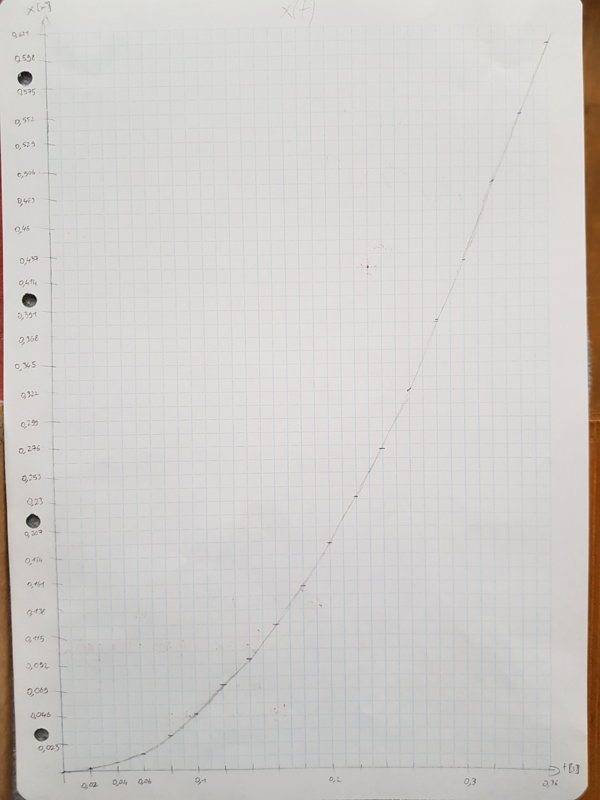
I got a curved line with the first one:

and a straight line with the x(t²) graphic:

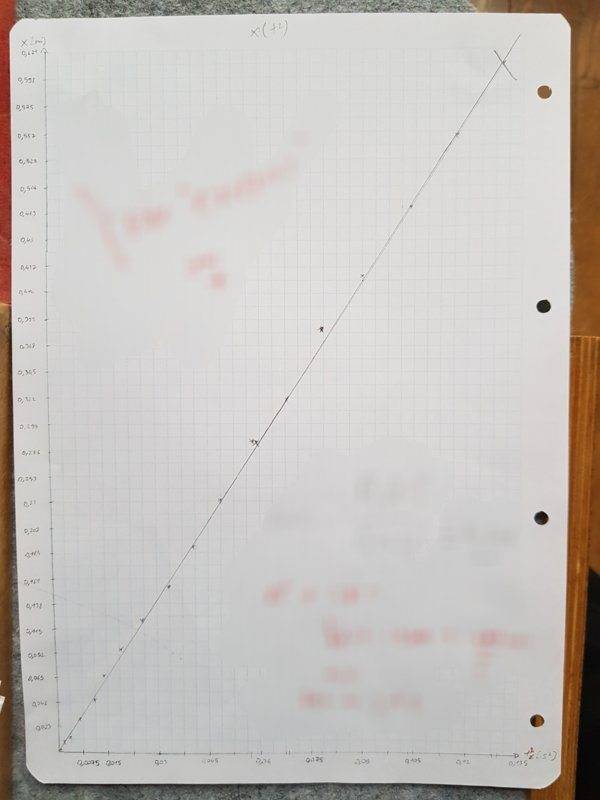
Here's my problem... We're told to first calculate the slope of this (x(t²))graphic. The expression to calculate a slope being Δy/Δx. The very last "position" (y axis) on the graphic is 0.610m at 0.1296s² (x axis).
0.610/0.1296 ≃ 4.708
Assuming that the slope = 4.708, how could I know find the acceleration from that ? The graphic being a constant straight line, isn't the acceleration = 0 ?
But that's not the case (a=9.81), if I'm not mistaken...

I am really sorry to bother you with a such a stupid question ! I really thank you in advance.

(ps.: I'm Swiss, sorry for my English...)

 

[phyzguy]

In the first graph, you plot x vs t, and you see the slope, which is Δx/Δt increasing. In the second graph, you plot x vs t^2, so the slope is Δx/Δ(t^2). Since an object moving with constant acceleration a follows the equation x = \frac{1}{2} a t^2, the slope of this line (Δx/Δ(t^2))is 1/2 a. This is just what you found. Does this help?

 

[Ellio]

In the first graph, you plot x vs t, and you see the slope, which is Δx/Δt increasing. In the second graph, you plot x vs t^2, so the slope is Δx/Δ(t^2). Since an object moving with constant acceleration a follows the equation x = \frac{1}{2} a t^2, the slope of this line (Δx/Δ(t^2))is 1/2 a. This is just what you found. Does this help?

Absolutely, it really helped me thank you a lot !