- #1
jackmell
- 1,807
- 54
Hi,
We have:
[tex]\beta(a,b)=\int_0^1 t^{a-1}(1-t)^{b-1}dt,\quad Re(a)>0, Re(b)>0[/tex]
and according to Wikipedia:
http://en.wikipedia.org/wiki/Pochhammer_contour
we can write:
[tex]\left(1-e^{2\pi ia}\right)\left(1-e^{2\pi ib}\right)\beta(a,b)= \int_P t^{a-1}(1-t)^{b-1}dt[/tex]
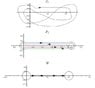
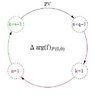
valid for all a and b where [itex]P[/itex] is the pochhammer contour given in the Wikipedia reference.I cannot find any type of derivation for this expression on the net. Would someone know how this is derived?Ok thanks,
Jack
We have:
[tex]\beta(a,b)=\int_0^1 t^{a-1}(1-t)^{b-1}dt,\quad Re(a)>0, Re(b)>0[/tex]
and according to Wikipedia:
http://en.wikipedia.org/wiki/Pochhammer_contour
we can write:
[tex]\left(1-e^{2\pi ia}\right)\left(1-e^{2\pi ib}\right)\beta(a,b)= \int_P t^{a-1}(1-t)^{b-1}dt[/tex]
valid for all a and b where [itex]P[/itex] is the pochhammer contour given in the Wikipedia reference.I cannot find any type of derivation for this expression on the net. Would someone know how this is derived?Ok thanks,
Jack
Attachments
Last edited: