Vircona
- 4
- 0
Hey, all,
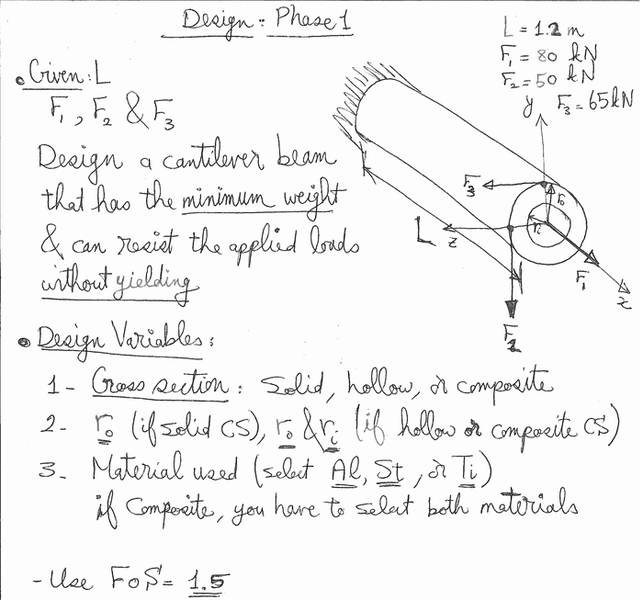
So I posted a similar thread yesterday about my project design issue, but I've made progress on it by taking a different approach. For the project, I have a cantilever shaft of fixed length (1.2m) and a tensile axial loading, and two torsional loadings in the same direction at different points on the outer edge of the shaft (opposite end of its support). I need to design the lightest-weight solid shaft that will withstand the forces without yielding due to stress.
I'm using a formula designed for this purpose:
c=((2/(π*τ))*√(M^2+T^2))^1/3
where c is radius, τ is allowable shearing stress, M is moment, and T is torque.
I have my maximum allowable shearing stress an have the equation for c set up in an excel file. The only issue I'm having is finding the highest combination of M and T, since the point of maximum moment and the point of maximum torque are unlikely to be the same. This point should give me the minimum allowable radius, which would obviously lead to the lightest shaft (I only have 3 materials to choose from, so I can check their weights vs. yield strengths manually).
Basically, can anyone help me find the largest value of M^2 + T^2 in a cantilever shaft?
EDIT: Note that the project PDF is shown below but has been changed. I'm ONLY concerned with a solid rod now -- not hollow or composite.
So I posted a similar thread yesterday about my project design issue, but I've made progress on it by taking a different approach. For the project, I have a cantilever shaft of fixed length (1.2m) and a tensile axial loading, and two torsional loadings in the same direction at different points on the outer edge of the shaft (opposite end of its support). I need to design the lightest-weight solid shaft that will withstand the forces without yielding due to stress.
I'm using a formula designed for this purpose:
c=((2/(π*τ))*√(M^2+T^2))^1/3
where c is radius, τ is allowable shearing stress, M is moment, and T is torque.
I have my maximum allowable shearing stress an have the equation for c set up in an excel file. The only issue I'm having is finding the highest combination of M and T, since the point of maximum moment and the point of maximum torque are unlikely to be the same. This point should give me the minimum allowable radius, which would obviously lead to the lightest shaft (I only have 3 materials to choose from, so I can check their weights vs. yield strengths manually).
Basically, can anyone help me find the largest value of M^2 + T^2 in a cantilever shaft?
EDIT: Note that the project PDF is shown below but has been changed. I'm ONLY concerned with a solid rod now -- not hollow or composite.