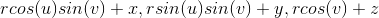Discussion Overview
The discussion revolves around the problem of drawing a circle perpendicular to a specified vector in 3D space, with a focus on the mathematical and programming approaches to achieve this. Participants explore various methods, including parametric equations and vector calculations, while addressing the complexities involved in defining the circle's position and orientation.
Discussion Character
- Exploratory
- Technical explanation
- Mathematical reasoning
- Debate/contested
Main Points Raised
- One participant suggests using the equation of a sphere centered at a point but seeks the relationship between parameters u and v to form a circle normal to a specified vector.
- Another participant proposes finding two orthogonal vectors to the specified vector using the cross-product, and then combining them with sine and cosine functions as in 2D.
- A different participant mentions the need for a plane normal to the vector and expresses uncertainty about how to find the constant D in the plane equation.
- One participant shares a link to a resource on parametric equations of a circle in 3D but expresses frustration with their implementation in code.
- Another participant provides a code snippet related to calculating circle points based on angles and a normal vector, indicating the complexity of their programming task.
- One participant discusses the use of the cross product to find a vector normal to the circle's surface, but does not clarify how this relates to the overall problem.
- Another participant references a Wolfram site that discusses the parameters needed for a circle in 3D, noting a potential error in the definitions of angles.
Areas of Agreement / Disagreement
Participants express varying approaches and methods to solve the problem, with no clear consensus on the best method or solution. Some participants agree on the necessity of finding orthogonal vectors and defining a plane, while others challenge the effectiveness of certain approaches, indicating ongoing debate.
Contextual Notes
Participants highlight the complexity of defining a circle in 3D, noting the need for multiple parameters and the challenges in programming implementations. There is also mention of potential errors in existing resources, which may affect understanding.
Who May Find This Useful
This discussion may be useful for computer programmers, mathematicians, and physics enthusiasts interested in 3D geometry, vector mathematics, and parametric equations.