How to find the exact value of cos 67.5 ?

[jkristia]

One of the questions in the homework for online precalc class I'm taking is to find the exact value for cos (67.5).
At first I didn't realize that I should just take the half angle of 135, so instead I tried to find the value for cos (45 + 45/2), and got stuck at this point.

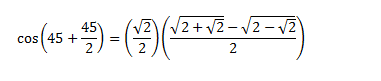
If I calculate the actual value I get the correct answer, but I'm not able to see how I can simplify this further.
I know the solution is as simple as finding the half angle value of

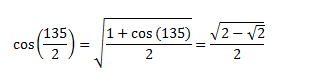
Any suggestions of how I can get from my first attempt solution to the simpler (and correct) solution?

 

[genericusrnme]

How is Cos(x) related to Cos(x+90), how is Cos(x+90) related to other trig functions?

 

[vela]

Try multiplying both the top and bottom by $\sqrt{2-\sqrt{2}}$.

 

[jkristia]

>>How is Cos(x) related to Cos(x+90), how
yeah, that definitely makes it simpler

>>Try multiplying both the top and bottom by
I have tried, but I seem to end up with a square root I can't get rid of, but I will keep trying.


Thanks for your help
Jesper

 

[ehild]

Hi, jkristia,

Square your formula for cos(45+45/2), simplify, and then take the square root.ehild

 

[jkristia]

Hi, jkristia,

Square your formula for cos(45+45/2), simplify, and then take the square root.


ehild

ah - of course, that works
Thank you very much