DavAeroEng
- 4
- 1
We know a way of measuring energy of a electromagnetic wave is the Poynting vector, which is independent of the frequency. But let's say we want to make two different electromagnetic waves, with different wavelengths and so different frequency, but with the same amplitude (so same Poynting vector).In my opinion the guy in the image is spending more energy for the wave with higher frequency. But the Poynting vector, doesn't care. So is there another property of Electromagnetic Waves that accounts for the energy that the guy used to make the wave?
Also think of it in terms of kinetic energy, let's say you have a rope attached to a rotating wheel. The rotational kinetic energy of the wheel is: K= 1/2 * I * w . I = 1/2 *m*r^2. w is the angular speed. We know w=2*pi*frequency. While r we could say is the same as the amplitude of the wave of the rope. Well it is pretty simple to see that the energy to make a higher frequency wave, is higher. Naturally also the amplitude has influence over the energy of the associated rope wave.
the en
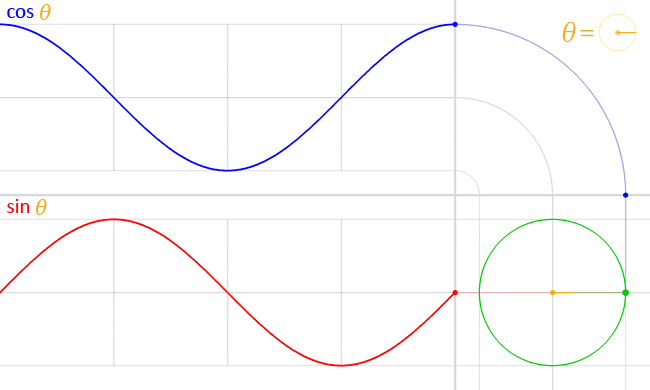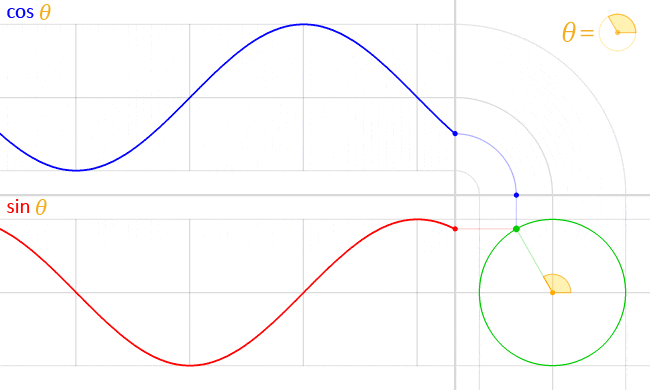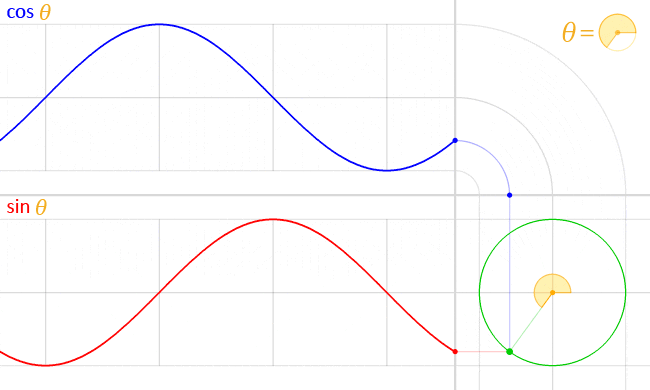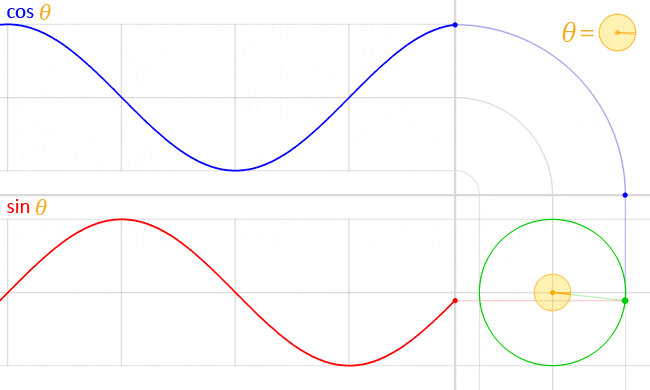
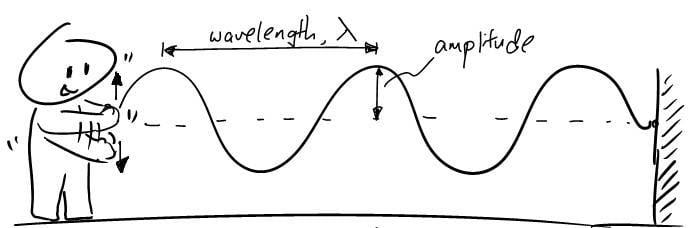
Also think of it in terms of kinetic energy, let's say you have a rope attached to a rotating wheel. The rotational kinetic energy of the wheel is: K= 1/2 * I * w . I = 1/2 *m*r^2. w is the angular speed. We know w=2*pi*frequency. While r we could say is the same as the amplitude of the wave of the rope. Well it is pretty simple to see that the energy to make a higher frequency wave, is higher. Naturally also the amplitude has influence over the energy of the associated rope wave.
the en