SUMMARY
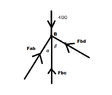
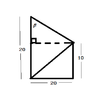
This discussion focuses on solving a statics truss problem at joint C using the Joint Method. The participants emphasize the importance of analyzing node B first, as it has only two unknown stresses, allowing for the calculation of stress at joint B ($F_{BC}$). Once $F_{BC}$ is known, the analysis of joint C becomes feasible with only two unknowns remaining. The discussion also touches on creating free body diagrams and calculating angles using trigonometric principles.
PREREQUISITES
- Understanding of statics and truss analysis
- Familiarity with the Joint Method for solving truss problems
- Ability to create and interpret free body diagrams
- Knowledge of basic trigonometry for angle calculations
NEXT STEPS
- Learn how to apply the Joint Method in truss analysis
- Study the creation of free body diagrams for complex structures
- Explore the method of sections for solving truss problems
- Review trigonometric principles for calculating angles in right triangles
USEFUL FOR
Students and professionals in civil engineering, mechanical engineering, and architecture who are involved in structural analysis and design of trusses.