Identifying Pin Joints & Rollers - Structural Analysis Homework Help

[Stephen Bulking]

Summary:: I am doing my structural analysis homework and I can't seem to identify between pin joint and roller.

Please take a look at the following exercises and help me understand:

1) In exercise 6.87, the joint at C is a pin joint whereas in exercise 5.63 the joints at the casters are rollers. I have solved these two problems check the answers, the assumptions I made about the joints are all correct. But the problem is they are all essentially a wheel with a PIN going through its center, how do I tell them apart? If they're not the same, please point out the difference.

2) I have added the two airplane exercises 5.67 and 5.27, and again with the same question the wheels of the airplane in 5.67 are rollers and I don't really know what joint I'm supposed to assign to the wheel in 5.27 (solving the problem does not require me to identify the joint at the wheel, I just hate it when I'm not on the same page with the book).

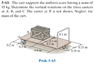
3) With question 1 answered, I'm still uncertain as to which joint I'm dealing with in exercise 6.84 (the truck) and how do I even draw a Free-body Diagram of the massive truck? I tried treating the wheels as rollers and did not succeed for not having enough equilibrium equations.

PS: I have included the support reactions of the joints (pin and roller) in 2D and 3D.

 

[BvU]

Hi,
1) in 5-63 all that is needed are the vertical forces. Pin or roller, one unknown.
In 6.87 the contraption collapse if the pin at C is replaced by a roller. I. e. there is a vertical force and a horizontal force.

2) 5-67 same story: wheels or struts, same answer. Ony vertical forces.
5-27: vertical force and horizontal force.

how do I even draw a Free-body Diagram of the massive truck? I tried treating the wheels as rollers and did not succeed for not having enough equilibrium equations

3) Do you need equations for the drawing ? What does your best shot at an FBD look like ?

And, completely separate (but preferably with a -- simplified -- drawing too ):

I tried treating the wheels as rollers and did not succeed for not having enough equilibrium equations

Wheels can roll, yes. Does it matter here ? Any non-vertical forces play a role ?
Can't comment on the possibly missing equations since you don't post what you have.

 

[Lnewqban]

For each case, you need to analize how many degrees of freedom each type of support restrains.
Please see:
https://en.m.wikipedia.org/wiki/Degrees_of_freedom_(mechanics)
The tires are free to move upwards, the pins are not.

The diagrams are sometimes confusing, but the general convention is that a pin support can also handle a reaction force acting away from the represented surface (please, see link to book).
https://books.google.com/books?id=nsQd5r7J6WkC&pg=PA63#v=onepage&q&f=false

In real structural applications, actual rollers couldn't do that, but the weights they support are huge compared to any lifting forces in most cases.
For exemptions, yes, some type of mechanical restriction to uplift is necessary.

Please, see also pages 9.1.17 and 9.1.18 of this link:
http://www.dot.state.oh.us/Division...pection and Evaluation of Bridge Bearings.pdf

I have seen diagrams that represent these situations with sliding collars instead.

The case of the truck can be solved, if you treat is as two independent bodies (note that the problem gives you each weight) that share one support.

 

[Stephen Bulking]

Hi,
1) in 5-63 all that is needed are the vertical forces. Pin or roller, one unknown.
In 6.87 the contraption collapse if the pin at C is replaced by a roller. I. e. there is a vertical force and a horizontal force.

2) 5-67 same story: wheels or struts, same answer. Ony vertical forces.
5-27: vertical force and horizontal force.
3) Do you need equations for the drawing ? What does your best shot at an FBD look like ?

And, completely separate (but preferably with a -- simplified -- drawing too ):
Wheels can roll, yes. Does it matter here ? Any non-vertical forces play a role ?
Can't comment on the possibly missing equations since you don't post what you have.

Thanks for replying quickly, I've read your comments and I still have questions:
1) Yes, in 5-63 and 5.67, "all that is needed TO SOLVE THE PROBLEM are the vertical forces". I HAVE SOLVED all of these problems and checked the answers (except for the truck, which doesn't come with an answer) so I can confirm that, but that is not the problem at hand. The problem is WHY and/or WHEN is it a roller/pin joint? In 5-63 and 5-67, I chose to treat the supporting wheels as ROLLERS, which would assign them with only one unknown vertical force but in 6-87 I treated the wheels as pin joints with 2 unknowns.
Also, how could you know that the contraption would collapse if the wheels are rollers (1 unknown)?

2) This contradiction is also apparent in 5-67 and 5-27: They both describe the wheels of an airplane but each does it differently??

3)No I don't need the equations to draw the Free-body diagram, I need the Free-body diagram to WRITE THE EQUATIONS. Here's what I have in mind for the truck: (see embedded pictures)

 

[Stephen Bulking]

For each case, you need to analize how many degrees of freedom each type of support restrains.
Please see:
https://en.m.wikipedia.org/wiki/Degrees_of_freedom_(mechanics)
The tires are free to move upwards, the pins are not.

The diagrams are sometimes confusing, but the general convention is that a pin support can also handle a reaction force acting away from the represented surface (please, see link to book).
https://books.google.com/books?id=nsQd5r7J6WkC&pg=PA63#v=onepage&q&f=false

In real structural applications, actual rollers couldn't do that, but the weights they support are huge compared to any lifting forces in most cases.
For exemptions, yes, some type of mechanical restriction to uplift is necessary.

Please, see also pages 9.1.17 and 9.1.18 of this link:
http://www.dot.state.oh.us/Division...pection and Evaluation of Bridge Bearings.pdf

I have seen diagrams that represent these situations with sliding collars instead.

The case of the truck can be solved, if you treat is as two independent bodies (note that the problem gives you each weight) that share one support.

Hi, thanks for replying so quickly, I have read your comments and I'm still a little fuzzy.
I do know and can tell the difference between the roller and pin joint, I just CAN'T IDENTIFY between them because like you said: "The figures are sometimes confusing". Please see my "heated" debate with BvU to understand exactly how these exercises and their figures confuse me.

You said : "the tires are free to move upward, the pins are not". To my understanding, the pin puts 2 translational constraints on the link (whatever is connected to it) and the roller places only one constraints which is "perpendicular to the surface at the point of contact"(See my embedded figures). I don't think the tires are free to move upward, if anything that should be the direction in which they're not allowed to move in cause of the constrain (roller or pin).

I had referred to the links you sent me but I can't access the last one, maybe cause I'm from another country? (I'm not very good with the Internet)

Oh and the truck, yes I treat it as two separate bodies connecting with each other through the pin D, here's my free-body diagram: (see embedded pictures)

 

[Lnewqban]

Perhaps you can read this one:
http://web.mit.edu/4.441/1_lectures/1_lecture13/1_lecture13.html

 

[Stephen Bulking]

Perhaps you can read this one:
http://web.mit.edu/4.441/1_lectures/1_lecture13/1_lecture13.html

Thank you, but what I don't understand here is not what joint goes with what reaction support. I understand how the pin joint has 2 constraints and the roller has only one. The problem is with the exercises that I included. Seems to me as if they're just switching between the two joints randomly. See exercise 5-27 and 5-67 that I posted, both discuss the wheel of the plane and each does so differently.
But let's turn a blind eye to that for a moment, I posted the free-body diagram of the truck exercise, please see whether that is correct or not. Thanks.

 

[BvU]

Do you recognize the truck in my version of the FBD ? ( hint: color )

​

​

Main differences with youre picture:​

The truck ends at D (So Na doesn't work on the truck) and​

the force that the tanker exerts on the truck is missing in your FBD​

Your tanker can never be in equilibrium: Dx must be zero (no other horizontal force present)​

and the normal force at A is missing.​

​

Agree ? then re-post the two FBDs​

​

Quiz: what does the xercise composer mean with the well meant 'D which acts as a pin': a horizontal pin or a vertical pin ?​

 

[BvU]

the contraption would collapse if the wheels are rollers

Did I say that ? This way we get a 'heated debat' based on misquoting !
The axle at C is a kind of pin a construction sense: it exerts a horizontal force and a vertical force. I suppose one should formally call it hinge. The presence of the wheel in the drawing has no significance for the analysis (there are only normal forces at the wheels -- the frame could just as well stand on the floor).

In a way I resent these quasi-realistic colorful figures: they hinder straight thinking.
But it's pretty customary nowadays to embellish textbooks with colorful, detailed and totally irrelevant embellishments

especially for engineers

On the other hand, in the old days they did something similar for physicists, too

 

[Stephen Bulking]

Do you recognize the truck in my version of the FBD ? ( hint: color )

​

View attachment 277723​

​

Main differences with youre picture:​

The truck ends at D (So Na doesn't work on the truck) and​

the force that the tanker exerts on the truck is missing in your FBD​

Your tanker can never be in equilibrium: Dx must be zero (no other horizontal force present)​

and the normal force at A is missing.​

​

Agree ? then re-post the two FBDs​

​

Quiz: what does the xercise composer mean with the well meant 'D which acts as a pin': a horizontal pin or a vertical pin ?​

Hi, your FBD is really helpful, I have never thought that the truck would end at D. I redraw the FBD of the tanker and the truck. If my FBDs are correct then the problem is solved.
I thought the force that the tanker exerts on the truck is Dy where they are connected. Since it's a pin connection so I included Dx in my figure, but of course since all forces are vertical, Dx is zero.

About your quiz, I'm not really sure what you mean by horizontal pin and vertical pin, or have ever been introduced to these concepts reading through the book (so far); But if I were to take a guess I'd say it's a horizontal pin going through D (into the page).

 

[Stephen Bulking]

Did I say that ? This way we get a 'heated debat' based on misquoting !
The axle at C is a kind of pin a construction sense: it exerts a horizontal force and a vertical force. I suppose one should formally call it hinge. The presence of the wheel in the drawing has no significance for the analysis (there are only normal forces at the wheels -- the frame could just as well stand on the floor).

In a way I resent these quasi-realistic colorful figures: they hinder straight thinking.
But it's pretty customary nowadays to embellish textbooks with colorful, detailed and totally irrelevant embellishmentsView attachment 277755

especially for engineers

On the other hand, in the old days they did something similar for physicists, too

View attachment 277756

Ohh, I see now. These figures ARE misleading. It's just like you said: "The presence of the wheel in the drawing has no significance for the analysis, the frame could just as well STAND on the floor". The exercise is a lot clearer to me with the image of the hoist STANDING.

But I just have to ask: if the wheel is SOMETIMES insignificant and can be treated as a stable "footing" (like in this case) and SOMETIMES it's a rolling wheel with only one vertical reaction force, how can one know when to treat it as what? Or is the figure of this one exercise just deceptive?

 

[BvU]

It's important for exercises like this not to be distracted (deceptive is a bit strong) by realistic rendering that doesn't play a role in the analysis. The landing gear in 5-67 could just as well be legs (standing gear ) or even ropes hanging from a (sturdy and huge ) ceiling -- the outcome would still be the same.

But in 5-27 there is a force with a direction given. Even there one can do without the wheel, as long as the two components are the same.

 

[Stephen Bulking]

It's important for exercises like this not to be distracted (deceptive is a bit strong) by realistic rendering that doesn't play a role in the analysis. The landing gear in 5-67 could just as well be legs (standing gear ) or even ropes hanging from a (sturdy and huge ) ceiling -- the outcome would still be the same.

But in 5-27 there is a force with a direction given. Even there one can do without the wheel, as long as the two components are the same.

Ok thanks again, I understand now.

 

[Lnewqban]

... The problem is with the exercises that I included. Seems to me as if they're just switching between the two joints randomly. See exercise 5-27 and 5-67 that I posted, both discuss the wheel of the plane and each does so differently.

Please, Stephen, excuse my poor understanding of the problem you had.

Discussing exercise 5-27:
Whenever a real wheel is in braking or accelerating mode, it can’t be considered to be a pure roller.

In any of those two dynamic cases, there is a force component aligned with the direction of the movement.
There is also an internal moment impossed on the structure to which the caliper of the brake is attached, reason for which you should not get into the difficult problem of internal forces in a problem like this.

The wheel is not free to roll forward, but the airplane may nose over around the wheel axis; therefore, you should consider its axis to be a pin or hinge, at least during the time the airplane is braking.

Once the airplane stops, the horizontal dynamic braking force of 2 KN disappears and the vertical static force of 6 KN remains (increasing the internal tension of strut AB).

Note that if the magnitude of the horizontal braking force were 2.18 KN instead (6 KN times tangent of 20°), then the tension in strut AB would become zero.
As it is only 2 KN, the real force at an angle of 18.4° respect to the vertical induces a clockwise rotation about pin C and internal tension forces in strut AB.

If a parking brake is applied to this wheel, and someone tries to push the airplane forward, a horizontal reaction will appear: we have a pin (this time relocated to the contact patch-pavement area).
If a parking brake is not applied to this wheel, and someone tries to push the airplane forward, a horizontal reaction will not appear: we have a roller (not a pure roller, as all real wheels resist to be pushed, at least a little).

Discussing exercise 5-67:
This could be compared to a triangular table with three legs, supporting a huge weight that is displaced from the centroid of the triangle; therefore, each leg will have to support a different percentage of the total weight.

Since all the involved forces are acting vertically (aligned with the z-axis), it does not matter whether or not there are casters between the legs and the floor.

In the case of the airplane represented in the diagram, a tow truck would be able to pull the airplane along the x-axis (parking brakes released), but not along the y-axis.

Respect to the x-axis we have rollers, respect to the y-axis we have pins or hinges (the landing gear structures are fixed at their top ends, but free to bend and to rotate a little at the contact patches of the tires).

For locating the center of mass of the whole airplane shown in the problem, where the total weight is acting, please, see:
http://hyperphysics.phy-astr.gsu.edu/hbase/cm.html#cmc

But let's turn a blind eye to that for a moment, I posted the free-body diagram of the truck exercise, please see whether that is correct or not. Thanks.

I believe that you have solved this one with the help of @BvU.

My calculations show 12000 lbf on axis A (probably 6000 per A-tire), 13100 lbf on axis B, and 2900 lbf on axis C.

Please, see a picture of the real turntable between truck and trailer.
Note the shaft (part #18) that allows rotation about the vertical plane, making impossible any transfer of moment between truck and trailer.

 

[Stephen Bulking]

OK man, Wow! I just can't imagine how much time and effort you put into my problems. I really appreciate this, thank you. Despite your hard work, I'm only a student and your thorough analysis of the problems are a little bit overwhelming for me. Of course that has never been the reason to give up :) , after reading through your thoughts on the problems, I wish to add a few comments to our discussion:

On problem 5-27
It was so clever of you to have pointed out the fact that the brakes are being applied, I didn't even notice that. I believe that was the key to my question. I completely agree with the conclusion that you have ultimately come to.

On problem 5-67
I find your way of thinking "it's a roller with respect to the x-axis (since a tow truck (very strong one) could pull it away in this direction) and a pin/hinge in with respect to the y-axis " a bit confusing at first but it then becomes reasonable and easy to relate to, though I'm not sure we're allowed to call 1 joint by two names (even if it's with respect to different axes) so I'm just going with roller here because only vertical forces are considered. Also why did you have to find the center of mass for this problem? I thought they have already given A,B,C as centers of mass and I could solve the problem without finding the entire system's center of mass.

On problem 6-84
Right I can't believe this is still bugging me :)
I was surprised by your answers, they did not match mine. How specifically did you section the truck? From BvU FBD, taking moment about point D would give me normal reaction at wheel C, that is:

\Sigma Mc = -8000*9 + Nc*14

=> Nc = 5142lb
With Nc being different, it goes without saying that our other two results would also not match. I used the FBD I included in my reply to BvU, which I've just realized does not include Normal reaction at wheel A, if you don't mind could you please show me yours as well?
Also your picture of the turntable made it a lot clearer for me how the tanker and the truck is connected, thanks. I understand how this would allow for rotation in the vertical Oxz plane (if Oy is directed out of the page towards us), but I'm not sure what you meant by " making impossible any transfer of moment between truck and trailer".

Anyway, thanks again for your time and effort, I really appreciate it.

 

[BvU]

On problem 6-84
Right I can't believe this is still bugging me :)
I was surprised by your answers, they did not match mine. How specifically did you section the truck? From BvU FBD, taking moment about point D would give me normal reaction at wheel C, that is:

$$\sum M_c = -8000*9 + Nc*14 \Rightarrow N_c = 5142 \ \text {lb}$$

Well done ! Can you find the small mistake in #14 ?

Anyway, thanks again for your time and effort, I really appreciate it.

Thank you and you are welcome. For us it's fun too (or else we wouldn't do it )

 

[Stephen Bulking]

Well done ! Can you find the small mistake in #14 ?

View attachment 277949​

Thank you and you are welcome. For us it's fun too (or else we wouldn't do it )

Well the only mistake I can think of is wrong notation: \Sigma Md not \Sigma Mc
But I did say that I was going to take moment sum about point D (equals to zero for equilibrium). Using the conventional ccw as the positive direction, I believe I've got all the signs (plus and minus) correct.
With your FBD of the rest of the truck, I have worked out the normal reaction forces at A to be 8000lb (taking moment sum about point D), which means Fd = 12000lb (equilibrium force equation). If my reaction at C is correct, which I doubt it would be, then Fb equals 14858lb.
Summing up the 3 normal reaction force at the wheels (Fa + Fb + Fc) yields 28000lb. This is the only verification that my answer is "maybe" correct, as Lnewqban had shown, he had a completely different combination of numbers that also add up to 28000lb.

 

[Lnewqban]

OK man, Wow! I just can't imagine how much time and effort you put into my problems. I really appreciate this, thank you. Despite your hard work, I'm only a student and your thorough analysis of the problems are a little bit overwhelming for me. Of course that has never been the reason to give up :) , after reading through your thoughts on the problems, I wish to add a few comments to our discussion:

You are very welcome, Stephen.
I enjoy doing this and helping students at least a little.
I respect your effort for learning new things.

On problem 5-27
It was so clever of you to have pointed out the fact that the brakes are being applied, I didn't even notice that. I believe that was the key to my question. I completely agree with the conclusion that you have ultimately come to.

Wheels with applied brakes are not the best way to present this type of problems, in my opinion.

On problem 5-67
I find your way of thinking "it's a roller with respect to the x-axis (since a tow truck (very strong one) could pull it away in this direction) and a pin/hinge in with respect to the y-axis " a bit confusing at first but it then becomes reasonable and easy to relate to, though I'm not sure we're allowed to call 1 joint by two names (even if it's with respect to different axes) so I'm just going with roller here because only vertical forces are considered. Also why did you have to find the center of mass for this problem? I thought they have already given A,B,C as centers of mass and I could solve the problem without finding the entire system's center of mass.

In most cases, hinges work on a plane only (think of a hinged door).
For working on more than one plane, they have to be “universal”, which means having a sphere (like a truck tow ball), or two hinges in one (like a Cardan coupling).
Please, see:
https://en.m.wikipedia.org/wiki/Universal_joint

I don’t know of any other way to calculate how much weight each of the three tires of the airplane would be carrying.
Again, this is not the best type of problem for your level; rather than loads distribution along a beam, here we have spatial load distribution on a plane.
That is what I tried to show with my little isometric diagram of the triangular table with wheeled legs.

On problem 6-84
Right I can't believe this is still bugging me :)
I was surprised by your answers, they did not match mine. How specifically did you section the truck? From BvU FBD, taking moment about point D would give me normal reaction at wheel C, that is:

\Sigma Mc = -8000*9 + Nc*14

=> Nc = 5142lb
With Nc being different, it goes without saying that our other two results would also not match. I used the FBD I included in my reply to BvU, which I've just realized does not include Normal reaction at wheel A, if you don't mind could you please show me yours as well?
Also your picture of the turntable made it a lot clearer for me how the tanker and the truck is connected, thanks. I understand how this would allow for rotation in the vertical Oxz plane (if Oy is directed out of the page towards us), but I'm not sure what you meant by " making impossible any transfer of moment between truck and trailer".

Anyway, thanks again for your time and effort, I really appreciate it.

My results for problem 6-84 were wrong.
Excuse me, I did the calculations mentally and made mistakes.
My re-calculations show 8000 lbf on axis A (probably 4000 per A-tire), 14900 lbf on axis B, and 5100 lbf on axis C.
Your calculated values are more precise.

What I meant by "making impossible any transfer of moment between truck and trailer":
Imagine a link chain, one link can pull the next one, but it can’t transfer any moment on the vertical or horizontal planes.
Sometimes, that characteristic is desirable because accidental bending loads can overwhelm a structure.

For example, at the moment our truck begins climbing a step hill, tires of axle B could be lifted away and lose contact with the pavement.
If our truck had no hinge at D, only axles A and C would be supporting the total weight of 28K lbf, and the increased span or distance between those supports would greatly increase the bending stress in the chassis.

Another example of usefulness of hinges or pins:
Note the hinge connection between the horizontal beam and the column in the picture of a shop crane.
Without that hinge, the beam would be able to transfer a moment onto the weld to the column (accidental moment due to the diagonal bar having too much or not enough tension and/or heavy load deforming the beam some).
The way it is, that same weld only “feels” a vertical force, which is much easier for it to handle and for the engineer to calculate (accidental moments are not, but they can be very destructive).

 

[Stephen Bulking]

Ok with your verification of the results for problem 6-84, I don't think I have any more questions on the problems, thanks.

On our moment transferring discussion, your example of the shop crane helped me a great deal in understanding moment transferring, but just to make sure, might I ask that: " Is it because the hinge connection restrains 2 rotary motions and all translational motion (in 3D), allowing only rotation about its (the hinge) axis that the accidental moment due to heavy loading (probably on the horizontal beam at the hook) is NOT transferred to the column?(because this moment does not cause rotation about the hinge axis)"

 

[Lnewqban]

Exactly!
Without that hinge, a horizontal beam that “smiles” under heavy load would create some undesired deflection and bending stress on the column.
Note that a second vertical hinge allows the horizontal beam to freely swing side to side.

 

[Stephen Bulking]

Ok, I understand now, thanks again for all your hard work.