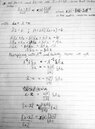How to Solve Condition Number and LU Decomposition Problems?

[akerman]

I have two question one of them I have solved but a bit differently and the second is something I need more help with. View attachment 2466

First question I have solved previously but bit different and I am not too sure how it should be solved in part b given above. Here is my similar solution View attachment 2467

Can you comment and show what should be done for part b and also for part c which I didn't know how to show.

P.S. I am preparing for my exams and this is not a coursework or anything in terms of homework. Therefore, explanation and comments what could be improved are good for me. Thanks

 

[I like Serena]

Hi akerman!

There is no mention in problem statement (b) of $\widetilde A$ or $\delta A$.
So it seems to me it should not be involved...

For (c), I would suggest to write:
$$a_{i,j} \overset ?= \sum_k l_{i,k} u_{k,j}$$
And write it out knowing that e.g. $l_{i,k} = 0$ unless $k=i$ or $k=i+1$.

 

[akerman]

Hi akerman!

There is no mention in problem statement (b) of $\widetilde A$ or $\delta A$.
So it seems to me it should not be involved...

For (c), I would suggest to write:
$$a_{i,j} \overset ?= \sum_k l_{i,k} u_{k,j}$$
And write it out knowing that e.g. $l_{i,k} = 0$ unless $k=i$ or $k=i+1$.

For (c) would it be enough to show the proof that product of two lower triangular matrices is still lower triangular and the same thing for upper triangular?

 

[I like Serena]

For (c) would it be enough to show the proof that product of two lower triangular matrices is still lower triangular and the same thing for upper triangular?

Those matrices are not just lower respectively upper triangular.
They are band matrices with specific values in the bands.
Any proof should take that into account and show that those specific values will match.

 

[CellCoree]

Hi there,

Thank you for reaching out. I would be happy to provide a response to your questions about condition number and LU decomposition.

First, let's briefly define what condition number and LU decomposition are. Condition number is a measure of how sensitive a mathematical problem is to changes in the input data. It is typically used to evaluate the stability and accuracy of numerical algorithms. On the other hand, LU decomposition is a method for decomposing a square matrix into a lower triangular matrix and an upper triangular matrix. It is often used to solve linear systems of equations.

Now, let's address your questions. For part b, I'm assuming you are given a matrix and asked to calculate its condition number. In this case, you would need to use the formula for condition number, which is the ratio of the largest singular value to the smallest singular value. You can find these singular values by performing a singular value decomposition (SVD) on the matrix. If you are not familiar with SVD, you can also use the formula for condition number in terms of the matrix's eigenvalues. This would involve finding the eigenvalues of the matrix and then taking the ratio of the largest eigenvalue to the smallest eigenvalue.

For part c, you mentioned that you were not sure how to show something. I'm not sure what you are referring to, so it would be helpful if you could provide more context or information. However, in general, to show something in mathematics, you would need to provide a proof or a logical explanation based on the definitions and properties of the concepts involved.

I hope this helps. Good luck with your exams! If you have any further questions, please don't hesitate to ask.