How to Solve Moment of Inertia for a Cylinder with Varying Radii?

[BernieCooke]

Homework Statement

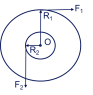
So I generally understand how to solve the following problem. My only roadblock is that I am not sure I am solving the moment of Inertia correctly. I know that for a solid cylinder you would use I = 1/2mr^2, but I am not sure how if it has only one mass given of 10 kg, yet the rod has a thicker radius at one point than another, you would solve for I. Any help would be greatly appreciated.A solid cylinder of mass 10 kg is pivoted about a frictionless axis through its center O. A rope wrapped around the outer radius R1 = 1.0 m, exerts a force of F1 = 5.0 N to the right. A second rope wrapped around another section of radius R2 = 0.50 m exerts a force of F2 = 6.0 N downward.
What is the angular acceleration of the disk?
If the disk starts from rest, how many radians does it rotate through in the first 5.0 s?

Homework Equations

torque = force x moment arm
torque = moment of inertia x angular acceleration
moment of inertia for a solid cylinder = 1/2 mass x radius squared

The Attempt at a Solution

I = 1/2 (10)(1)^2 for the first section of cylinder which gives 5 for moment of inertia
I = 1/2 (10)(.5)^2 for the section section which gives 1.25 for moment of inertia
combined = 6.25

 

[gneill]

The object is not a simple disk if it has different radii at different locations. Is there other information about the object that you haven't included? Was a diagram included?

 

[haruspex]

I gather the axis is horizontal. Assuming the density of the rod is uniform, you need to know what the lengths are at the two different radii. It is also not possible to tell from your description whether the two torques act together or oppositely.

 

[BernieCooke]

The object is not a simple disk if it has different radii at different locations. Is there other information about the object that you haven't included? Was a diagram included?

Sorry for the late reply. I was gone for the weekend. There was a diagram included and I have included it in this post. It appears to me that while it is a solid cylinder, the information about how the mass is distributed across two sections of different radii is excluded.

 

[gneill]

Okay, the image doesn't help with the mass distribution so I suppose you are forced to consider the object as a simple disk. Perhaps the inner part is to be considered a mass-less pulley affixed to the disk.

You should have only a single moment of inertia to deal with, but two torques.