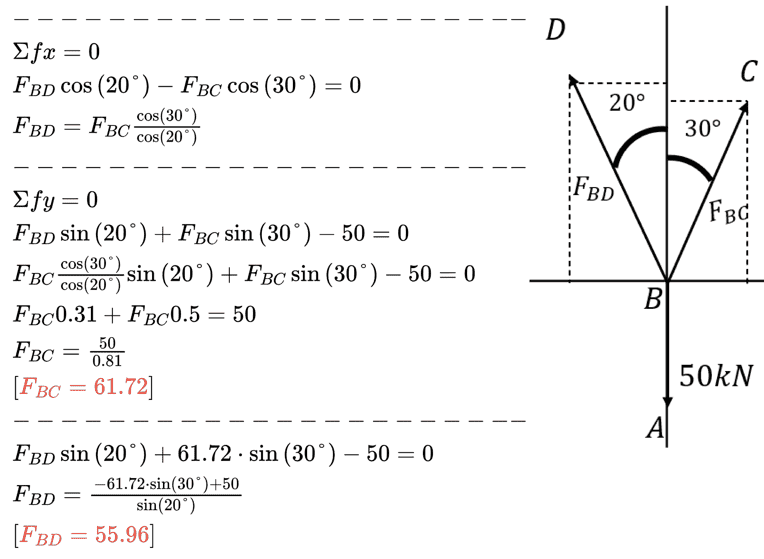How to solve this balancing exercise? (towing a boat with two ropes)

[Tapias5000]

Homework Statement

The towing pendant AB is subjected to the force of 50 kN exerted by a tugboat. Determine the force in each of the bridles, BC and BD, if the ship is moving forward with constant velocity.

Relevant Equations

Σfx=0 and Σfy=0

This is the image of the problem

I tried to solve it and I got the following is it correct?

 

[Delta2]

Your method seems correct in general . Haven't check the arithmetic operations.

BTW why don't you use the first equation you found for $F_{BD}$ to calculate it , once you have found $F_{BC}$ and you instead using a different equation?

 

[Delta2]

Oops I now see a flaw, you haven't labeled the x and y-axis explicitly, but it seems to me that the force of 50kN is acting in the x-direction... Though that would imply that the x-axis is the vertical and the y-axis is the horizontal.

 

[Tapias5000]

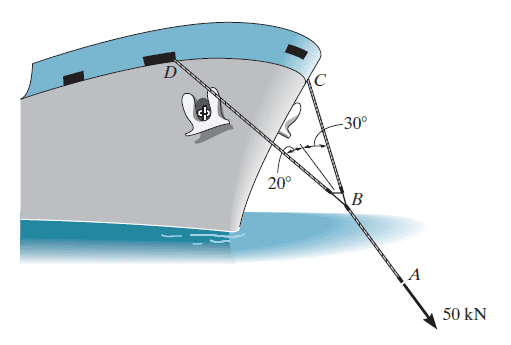
Oops I now see a flaw, you haven't labeled the x and y-axis explicitly, but it seems to me that the force of 50kN is acting in the x-direction... Though that would imply that the x-axis is the vertical and the y-axis is the horizontal.

um the force acts in the direction of x?
So in the directions change? I don't understand, why does that happen, can you show me some other example?
The answer then would be like this? but why?

$\begin{array}{l}----------------------\\ Σfx=0\\ -F_{BD}\sin \left(20°\right)+F_{BC}\sin \left(30°\right)=0\\ F_{BC}=F_{BD}\frac{\sin \left(20°\right)}{\sin \left(30°\right)}\\ ----------------------\\ Σfy=0\\ F_{BD}\cos \left(20°\right)+F_{BC}\cos \left(30°\right)-50=0\\ F_{BD}\cos \left(20°\right)+F_{BD}\frac{\sin \left(20°\right)}{\sin \left(30°\right)}\cos \left(30°\right)-50=0\\ F_{BD}0.93+F_{BD}0.59=50\\ F_{BD}=\frac{50}{1.52}\\ \left[F_{BD}=32.89\right]\\ ----------------------\\ F_{BD}\cos \left(20°\right)+F_{BC}\cos \left(30°\right)-50=0\\ 32.89\cdot \cos \left(20°\right)+F_{BC}\cos \left(30°\right)-50=0\\ F_{BC}=\frac{-32.89\cdot \cos \left(20°\right)+50}{\cos \left(30°\right)}\\ \left[F_{BC}=22.04\right]\\ ----------------------\end{array}$

 

[Delta2]

Yes I think now it is correct.

 

[Tapias5000]

Yes I think now it is correct.

ok, but how did you realize that the force acted on the x-axis and therefore the directions were changed? what did you look at to reach that conclusion?

 

[Delta2]

ok, but how did you realize that the force acted on the x-axis and therefore the directions were changed? what did you look at to reach that conclusion?

If I ask you to draw the force components that correspond to $F_{BC}\cos 30$ and $F_{BD}\cos 20$ where would you draw them, on the vertical axis or on the horizontal axis?

 

[Tapias5000]

If I ask you to draw the force components that correspond to $F_{BC}\cos 30$ and $F_{BD}\cos 20$ where would you draw them, on the vertical axis or on the horizontal axis?

According to me they would go on the red arrows, cosine= a/h

 

[Delta2]

Nope that's not correct, check again the definition of cosine for a right triangle.

 

[Tapias5000]

Nope that's not correct, check again the definition of cosine for a right triangle.

aaaaaaaaa, damn I finally understand regarding the angle would be here for cosine, and that's why the directions change, am I right now?

 

[Delta2]

Yes you are correct now.

 

[Tapias5000]

Yes you are correct now.

Thank you very much for the clarification.