How to Visualize Vectors and Subspaces in a Coordinate System?

[mathmari]

Hey!

We have the basis $B=\left \{\begin{pmatrix}1 \\ 1 \\ 1\end{pmatrix},\begin{pmatrix}2 \\ 1 \\ 0\end{pmatrix}, \begin{pmatrix}1 \\ 2 \\ 1\end{pmatrix} \right \}$ of $\mathbb{R}^3$ and the vector $v$ can we written as a linear combination of the elements of the basis as follows:
\begin{equation*}v=\begin{pmatrix}2 \\ 8 \\ -1\end{pmatrix}=-\frac{17}{2}\begin{pmatrix}1 \\ 1\\ 1\end{pmatrix}+\frac{3}{2}\begin{pmatrix}2 \\ 1\\ 0\end{pmatrix}+\frac{15}{2}\begin{pmatrix}1 \\ 2\\ 1\end{pmatrix}\end{equation*}

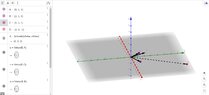
It is asked to visualize that in a coordinate system, by showing how the vector $v$ is generated by the basis.

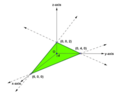
For that do we draw the three vectors of the basis and the vector $v$ or do we have to draw also the multiples of the elements of the basis that we use at the linear combination? (Wondering)

I mean, is the following enough?

View attachment 8601

(Wondering)
Further, we have the subspace $U=\left \{\begin{pmatrix}a \\ a+b \\ 2a-b\end{pmatrix}\middle| a, b\in \mathbb{R}\right \}$ of $\mathbb{R}^3$. How could we sketch $U$ in a coordinate system? (Wondering)

 

[I like Serena]

It is asked to visualize that in a coordinate system, by showing how the vector $v$ is generated by the basis.

For that do we draw the three vectors of the basis and the vector $v$ or do we have to draw also the multiples of the elements of the basis that we use at the linear combination? (Wondering)

I mean, is the following enough?

That's a bit subjective.
Since it says 'showing how the vector $v$ is generated by the basis', I'm inclined to say that we should do a bit more.
So yes, we could draw also the multiples of the elements of the basis that we use at the linear combination.
Or alternatively, in addition to the basis itself, we could draw all the lines of the parallellepipedum.

Here's a couple of examples how we might do it:

Further, we have the subspace $U=\left \{\begin{pmatrix}a \\ a+b \\ 2a-b\end{pmatrix}\middle| a, b\in \mathbb{R}\right \}$ of $\mathbb{R}^3$. How could we sketch $U$ in a coordinate system? (Wondering)

Here's a couple of examples how to sketch a plane.

Draw a rectangle with a couple of vectors to show how the vectors relate to the plain:

Draw the intersections with the coordinate planes:
View attachment 8602

 

[mathmari]

That's a bit subjective.
Since it says 'showing how the vector $v$ is generated by the basis', I'm inclined to say that we should do a bit more.
So yes, we could draw also the multiples of the elements of the basis that we use at the linear combination.
Or alternatively, in addition to the basis itself, we could draw all the lines of the parallellepipedum.

Which way do you suggest? The one with the parallellepipedum?

And how did you make these sketches? Is there a programm for that?

(Wondering)

Here's a couple of examples how to sketch a plane.

Draw a rectangle with a couple of vectors to show how the vectors relate to the plain:Draw the intersections with the coordinate planes:

Could you explain to me further these two sketches? (Wondering)

 

[I like Serena]

Which way do you suggest? The one with the parallellepipedum?

And how did you make these sketches? Is there a program for that?

I just copied them after googling.

And sure, there are plenty of programs to make sketches like these.
Didn't you already use one for post #1?
We can probably find a free online one.

Nowadays I would do it with Latex myself (TikZ).
Like this:
\begin{tikzpicture}[>=stealth']
%preamble \usepackage{tikz-3dplot}
%preamble \usetikzlibrary{arrows}
\tdplotsetmaincoords{60}{100}
\begin{scope}[scale=0.6,tdplot_main_coords]
\coordinate (O) at (0,0,0);
\coordinate (P) at (2,8,-1);
\coordinate (A) at ({-17/2},{-17/2},{-17/2});
\coordinate (B) at ({3},{3/2},{0});
\coordinate (C) at ({15/2},{15},{15/2});

\draw[help lines,->] (O) -- (8,0,0) node[anchor=north east]{$x$};
\draw[help lines,->] (O) -- (0,8,0) node[anchor=north west]{$y$};
\draw[help lines,->] (O) -- (0,0,8) node[anchor=south]{$z$};

\draw[->] (O) -- (A);
\draw[->] (A) -- ++(B);
\draw[->] (A) ++(B) -- ++(C);

\draw[ultra thick,->] (O) -- (1,1,1) node[anchor=south west]{$b_1$};
\draw[ultra thick,->] (O) -- (2,1,0) node[anchor=north west]{$b_2$};
\draw[ultra thick,->] (O) -- (1,2,1) node[anchor=south]{$b_3$};

\draw[ultra thick,->,color=red] (O) -- (P) node[anchor=west] {$v$};
\end{scope}
\begin{scope}[scale=0.6,xshift=15cm,tdplot_main_coords]
\coordinate (O) at (0,0,0);
\coordinate (P) at (2,8,-1);
\coordinate (A) at ({-17/2},{-17/2},{-17/2});
\coordinate (B) at ({3},{3/2},{0});
\coordinate (C) at ({15/2},{15},{15/2});

\draw[->] (O) -- (8,0,0) node[anchor=north east]{$x$};
\draw[->] (O) -- (0,8,0) node[anchor=north west]{$y$};
\draw[->] (O) -- (0,0,8) node[anchor=south]{$z$};

\draw[help lines] (O) -- (A) -- +(B) (A) -- ++(C) -- (P);
\draw[help lines] (O) -- (B) -- +(C) (B) -- ++(A) -- (P);
\draw[help lines] (O) -- (C) -- +(A) (C) -- ++(B) -- (P);

\draw[ultra thick,->] (O) -- (1,1,1) node[anchor=south west]{$b_1$};
\draw[ultra thick,->] (O) -- (2,1,0) node[anchor=north west]{$b_2$};
\draw[ultra thick,->] (O) -- (1,2,1) node[anchor=south]{$b_3$};

\draw[ultra thick,->,color=red] (O) -- (P) node[anchor=west] {$v$};
\end{scope}
\end{tikzpicture}

Could you explain to me further these two sketches? (Wondering)

For the first we would draw the 2 vectors that are in the plane.
And then draw a rectangle around it aligned with those vectors.
Since your plane intersects the origin, there is no need to draw a vector from the origin to the plane. (Thinking)

For the second, we would need to figure out the intersections of the plane with each of the coordinate planes.
That is, solve for $x=0$, respectively $y=0$, respectively $z=0$.
That should yield 3 vectors, which we can draw as lines.
We can color the area where it's between the coordinate axes as shown in the picture. (Thinking)

 

[mathmari]

And sure, there are plenty of programs to make sketches like these.
Didn't you already use one for post #1?
We can probably find a free online one.

Nowadays I would do it with Latex myself (TikZ).

Ah ok! In the first post I used Geogebra, so if I use this program I will draw the three elements of the basis $b_1, b_2, b_3$, then $-\frac{17}{2}b_1$, $\frac{3}{2}b_2$, $\frac{15}{2}b_3$ and then the sum of these ones? (Wondering)

For the first we would draw the 2 vectors that are in the plane.
And then draw a rectangle around it aligned with those vectors.
Since your plane intersects the origin, there is no need to draw a vector from the origin to the plane. (Thinking)

So, we draw the two vectors of the basis $\begin{pmatrix}1 \\ 1\\ 2\end{pmatrix}, \begin{pmatrix}0 \\ 1\\ -1\end{pmatrix}$, then we draw a rectangle that passes through the two endpoints of these vectors and the origin, since it is contained in $U$.

Have I understood that correctly? (Wondering)

 

[I like Serena]

Ah ok! In the first post I used Geogebra, so if I use this program I will draw the three elements of the basis $b_1, b_2, b_3$, then $-\frac{17}{2}b_1$, $\frac{3}{2}b_2$, $\frac{15}{2}b_3$ and then the sum of these ones?

I see you can use [M]Vector(<start point>, <end point>)[/M].
It means that we can also start the second vector at the end of the first one, can't we?

And if we want to draw a parellellepipedum, we can use [M]Line(<point>, <point>)[/M], can't we? (Wondering)

Or else we can indeed draw the vectors you mentioned. (Doh)

So, we draw the two vectors of the basis $\begin{pmatrix}1 \\ 1\\ 2\end{pmatrix}, \begin{pmatrix}0 \\ 1\\ -1\end{pmatrix}$, then we draw a rectangle that passes through the two endpoints of these vectors and the origin, since it is contained in $U$.

Have I understood that correctly?

I'd draw a rectangle, actually a rhombus, that is a bit bigger, but yeah, that's basically it.

Btw, did you try [M]Plane(...)[/M] in geogebra?
It pops up 6 different methods to define a plane... and then geogebra will draw it for you! (Muscle)

 

[mathmari]

I see you can use [M]Vector(<start point>, <end point>)[/M].
It means that we can also start the second vector at the end of the first one, can't we?

And if we want to draw a parellellepipedum, we can use [M]Line(<point>, <point>)[/M], can't we? (Wondering)

Or else we can indeed draw the vectors you mentioned. (Doh)

So, you mean to draw the vector $-\frac{17}{2}b_1$, then at the endpoint of that one we start the vector $\frac{3}{2}b_2$, then at the endpoint of that one we start the vector $\frac{15}{2}b_3$ and then we draw a vector from the origin to the endpoint of the last vector.

Or did you mean something else? (Wondering)

I'd draw a rectangle, actually a rhombus, that is a bit bigger, but yeah, that's basically it.

Btw, did you try [M]Plane(...)[/M] in geogebra?
It pops up 6 different methods to define a plane... and then geogebra will draw it for you! (Muscle)

Ok! (Nerd)

 

[I like Serena]

So, you mean to draw the vector $-\frac{17}{2}b_1$, then at the endpoint of that one we start the vector $\frac{3}{2}b_2$, then at the endpoint of that one we start the vector $\frac{15}{2}b_3$ and then we draw a vector from the origin to the endpoint of the last vector.

Or did you mean something else?

(Nod)