How to work around this equation giving infinities in the numerical calculation?

[FQVBSina_Jesse]

TL;DR

Heat conduction solution using Green's function has exponential and erfc terms. At boundaries, exponential gives infinity and other boundaries, erfc gives 0, making log transform difficult.

The heat conduction equation for a semi-infinite slab with a boundary condition of the first kind is as follows:

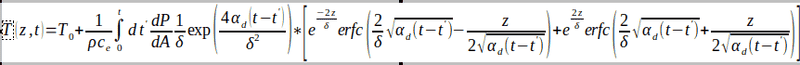
The problem is delta is a very small number, so the first exponential will tend to infinity. I am programming this in Fortran and it can accommodate values up to magnitude of 310, but beyond that, the code simply returns infinities. If the program does not simply return infinity, the exponential and erfc terms balance each other and generates a reasonable value.

If I apply the log transformation on the integrand, that will solve the problem of the delta squared. But the complimentary error functions at the boundary of z = 0 will give erfc(2/delta*sqrt(...)) = 0, which under log will return negative infinity.

Does anyone have a suggestion as to how I can resolve this issue? Thanks!

 

[Office_Shredder]

I don't know about this specific application, but the natural thing to do would be to expand things as Taylor series of delta, watch the infinities cancel out, and then keep whatever constant term is left over.

Assuming that's what's actually happening here.

 

[hunt_mat]

Try a transformation u=\tan^{-1}x. That should map everything onto a finite region.

 

[Haborix]

Can you try redefining the variables $t, t', z$ to absorb the $\delta$? It looks like once you do that the upper limit on your integral will get large, but it should take all dependence on $\delta$ out of the integrand.

 

[pasmith]

Can you scale your variables so that \delta \approx 1? That would be the usual way of handling this.