I deriving a pupil function in a coherent imaging system

Click For Summary
The discussion focuses on deriving the pupil function for a coherent imaging system, specifically involving a circular aperture and three 2-D delta functions. The original poster seeks guidance on building the coherent transfer function and expresses confusion about the process. Participants confirm the approach and provide reassurance about the correctness of the pupil function concept. The conversation emphasizes the importance of understanding the relationship between the pupil function and the coherent transfer function in imaging systems. Overall, the thread highlights the need for clarity in deriving these functions in optical systems.
silentt
Messages
2
Reaction score
0
Homework Statement
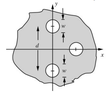
The aperture is opaque with 3 circular holes, each with a diameter of w. The coordinates of the center of the circular apertures are: {0, d/2}, {0, -d/2}, {d/2, 0}.
Derive the coherent transfer function.
Relevant Equations
{0, d/2}, {0, -d/2}, {d/2, 0}
Hello all. I have a question about building the coherent transfer function and specifically how I would go about deriving the pupil function for this figure. I have not come across this in my class yet and am a bit stumped.
Any help would be appreciated.
 

Attachments

  • Untitled21.png
    Untitled21.png
    6.2 KB · Views: 167
Physics news on Phys.org
the pupil would be a circular aperture and 3 2-d delta functions
 
Awesome, thanks for confirming my suspicions.
 

Thread 'Help needed with Elliptic Integrals'

I want to find the solution to the integral ##\theta = \int_0^{\theta}\frac{du}{\sqrt{(c-u^2 +2u^3)}}## I can see that ##\frac{d^2u}{d\theta^2} = A +Bu+Cu^2## is a Weierstrass elliptic function, which can be generated from ##\Large(\normalsize\frac{du}{d\theta}\Large)\normalsize^2 = c-u^2 +2u^3## (A = 0, B=-1, C=3) So does this make my integral an elliptic integral? I haven't been able to find a table of integrals anywhere which contains an integral of this form so I'm a bit stuck. TerryW
View full post »

Similar threads

I Why do we use low-coherence light in Optical Coherence Tomography?
  • · Replies 1 ·
Replies
1
Views
3K
Image Theory for an Electric Dipole
  • · Replies 14 ·
Replies
14
Views
2K
A rather weird form of a coherent state
  • · Replies 5 ·
Replies
5
Views
2K
I Paraxial ray tracing: fixing image/height w/o knowing stop location
  • · Replies 3 ·
Replies
3
Views
2K
Minimum Tone Spacing: Coherent Frequency Shift Keying
  • · Replies 17 ·
Replies
17
Views
4K
Complex Degree of Coherence (Cittert-Zernike)
  • · Replies 1 ·
Replies
1
Views
3K
Depletion width of linearly doped PN-junction
  • · Replies 1 ·
Replies
1
Views
1K
I Mathematical proof for the Lagrangian function
  • · Replies 4 ·
Replies
4
Views
1K
The equipotential surface of a system of two unequal charges
  • · Replies 3 ·
Replies
3
Views
2K
On charge image method over a conducting sphere and its Char
  • · Replies 6 ·
Replies
6
Views
3K