Homework Help Overview
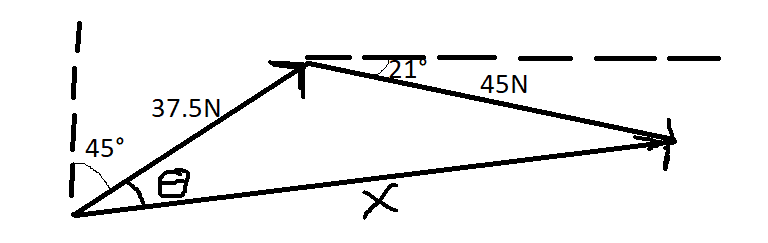
The discussion revolves around finding the resultant of two vectors: 37.5N directed northeast and 45N at an angle of 21° south of east. The original poster expresses difficulty in determining the angles necessary for calculating the resultant.
Discussion Character
- Exploratory, Assumption checking, Problem interpretation
Approaches and Questions Raised
- Participants discuss the need to find angles within the triangle formed by the vectors to calculate the resultant. Some suggest projecting vectors and questioning the angle between them. Others mention using the tip-to-tail method and vector components instead of relying solely on angles.
Discussion Status
There is an ongoing exploration of different methods for finding the resultant. Some participants have provided guidance on using vector components and the tip-to-tail method, while others have shared their own experiences and approaches. The discussion reflects a variety of interpretations without reaching a consensus.
Contextual Notes
Participants note the importance of showing effort in problem-solving as per forum rules. There is also mention of the law of cosines and its relationship to the dot product, indicating varying levels of familiarity with these concepts among participants.