- #1
Phi6er
- 4
- 0
First, I'll give a little background so you guys know why I've arrived at this issue. I'm writing my BSc thesis right now, and the point of the thesis is to predict the bound states of two-nucleon systems (one bound, others not) by treating the problem as a simple QM two body problem. With a potential that only cares about distance (the potential is spherically symmetric), the problem reduces to solving the radial Schrödinger equation, which is essentially the same problem as solving a 1D Schrödinger equation (with an "effective potential"). I have a numerical algorithm that can solve 1D Schrödes. I was thinking that I would use the one-pion exchange potential (OPEP) to represent the nuclear force, but later I realized that it actually has a tensor component. So then I decided to go with the simple Yukawa potential... but then I realized that that actually does not differentiate between nucleons at all (no spin or isospin dependence at all) and would hence give the same energies for dineutron and deuteron. Using the Yukawa potential is still a backup plan I suppose, but if I use it, I can't demonstrate how the exclusion princible together with the NN interaction's spin-dependence prevents the dineutron (and hence also the diproton) from being bound, which is the whole point of the thesis.
And that concludes the general description of the problem. Now let's get to the specifics! (Sorry about using pictures instead of the equation editor; I'm new and I don't know how that stuff works yet.)

If I've understood correctly, the dot product of the two spin matrices is either 1 (for a triplet spin) or -3 (for a singlet spin). Earlier in the same paper we also see this:
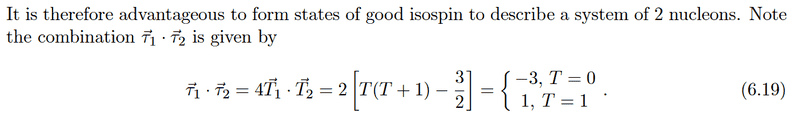
... so I can also understand what the product thing with the taus is! I'm still not confident that I understand isospin though, so let me just confirm a few things: the deuteron can have either T = 0 or T = 1, but diproton and dineutron can only have T = 1, right? Is that the way it works?
And the deuteron bound state is with T = 0 and S = 1, so that (τ1.τ2) = -3, and (σ1.σ2) = 1, right?
Also, setting S12 to zero makes OPEP specifically depend on (τ1.τ2)*(σ1.σ2), which is more than dubious since it works out the same for the deuteron ground state (T = 0, S = 1) as for dineutron and diproton (T = 1, S = 0).
If I can't make OPEP work... then what?
For example, is there some spin-dependent term I could for just add with the simple Yukawa potential?
And if none of this works out, then what kind of reasoning am I going to use to show that the dineutron is not bound, if I've just shown independently of spin and isospin that the deuteron has a bound state?
I've been spending way too much time on trying to figure this one out. I should already be quite a bit into writing the damn thesis already but this problem is stumping me hard. Any advice would be greatly appreciated. I'm all ears, and thanks in advance!
And that concludes the general description of the problem. Now let's get to the specifics! (Sorry about using pictures instead of the equation editor; I'm new and I don't know how that stuff works yet.)
- Would it make sense to average OPEP over all directions to ignore the angle dependence and hence get a spin-dependent spherically symmetric potential? If yes, how?
If I've understood correctly, the dot product of the two spin matrices is either 1 (for a triplet spin) or -3 (for a singlet spin). Earlier in the same paper we also see this:
... so I can also understand what the product thing with the taus is! I'm still not confident that I understand isospin though, so let me just confirm a few things: the deuteron can have either T = 0 or T = 1, but diproton and dineutron can only have T = 1, right? Is that the way it works?
And the deuteron bound state is with T = 0 and S = 1, so that (τ1.τ2) = -3, and (σ1.σ2) = 1, right?
- Can I just set the tensor part of OPEP to zero?
Also, setting S12 to zero makes OPEP specifically depend on (τ1.τ2)*(σ1.σ2), which is more than dubious since it works out the same for the deuteron ground state (T = 0, S = 1) as for dineutron and diproton (T = 1, S = 0).
If I can't make OPEP work... then what?
For example, is there some spin-dependent term I could for just add with the simple Yukawa potential?
And if none of this works out, then what kind of reasoning am I going to use to show that the dineutron is not bound, if I've just shown independently of spin and isospin that the deuteron has a bound state?
I've been spending way too much time on trying to figure this one out. I should already be quite a bit into writing the damn thesis already but this problem is stumping me hard. Any advice would be greatly appreciated. I'm all ears, and thanks in advance!
Attachments
Last edited: