JerusalemLuver
- 11
- 0
Hi, this question is a part of an 'online homework packet I received through my IB 11 SL course (ie. International Baccalaureate 11 Standard Leval). I submitted my first attempt to answer this question and had the wonderful "sorry your answer is incorrect" screen pop up. I was wondering if I could get some advice on howe to solve the question. Am I understanding the concept but doing something wrong when it comes to calculations? Or do I need a push in the right direction with concept?
Thanks
JL
1.

2.
3.
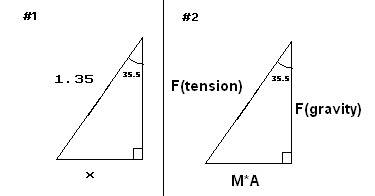
I first tried to calculate the radius adding the bottom part of the first triangle to half of the diameter.I'm fairly certain of the radius but if anyone thinks up another method or thinks that this method is incorrect please let me know.
I secondly calculated the Force of gravity on the 10 kg seat
Using the second triangle I used trig to solve for the total force
I then substituted the Total force (ie. Mass * Acceleration) and mass to solve for Acceleration.
Thanks
JL
1.
2.
- (Total Force) = mass * acceleration
- (Centrepital Acceleration) = (Velocity squared) / (Radius)
- (Force of Gravity) = (mass)*(9.8)
- (Radius) = (Diameter)/2
3.
- Using trig. Radius = (sin35.5 *1.35) + (diameter/2) =6.43394899 m
- (Force of Gravity) = 9.8 * 10 kg = 98 N
- Using trig (Total Force) = mass*acceleration = (tan 35.5 *Force of Gravity)= 69.990272065
- (Acceleration) = (Total Force)/mass = 69.990272065/10 =6.9990272065 m/s^2
I first tried to calculate the radius adding the bottom part of the first triangle to half of the diameter.I'm fairly certain of the radius but if anyone thinks up another method or thinks that this method is incorrect please let me know.
I secondly calculated the Force of gravity on the 10 kg seat
Using the second triangle I used trig to solve for the total force
I then substituted the Total force (ie. Mass * Acceleration) and mass to solve for Acceleration.
