How Do You Identify Spectral Lines and Calculate Fine Structure Constants?

[John Greger]

Homework Statement

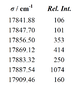
The Ca spectrum below, recorded using a Fourier Transform Spectrometer (FTS), shows the resolved $3d4s ^3D - 3d4p ^3D$ multiplet. The wavenumbers and their relative intensities are given in the table. Identify all the lines and determine the fine structure constants in the two triplets (both are positive).

Homework Equations

[/B]
$$I=F_{max} - J (1)$$

Landé interval rule: $\frac{F_{max}}{F_{max-1}} =$energy ratio between the F numbers(2)

$$ E_{hfs} = A/2 * [F(F+1) - J(J+1)-I(I+1)] (3)$$

The Attempt at a Solution

[/B]
I can determine the quantum numbers F,,J,I. But how do I know what rel. int. correspond to what transition?
And once I have the transitions. How do I use eq.(3) to solve for A?

Very grateful for any reply!

 

[mfb]

The relative intensity doesn't help you much here I think, but you can work with the energies.

 

[John Greger]

The relative intensity doesn't help you much here I think, but you can work with the energies.

Thanks!

I see. But how do I know what energy belong to what set of quantum numbers?

 

[mfb]

You have formulas for the energies of the different levels. The transitions correspond to differences between these energies. If you have states with energies E1, E2 and E3 in ascending order, then in general you expect transitions with energy (E2-E1), (E3-E2) and (E3-E1). You won't necessarily see all in your spectrum and you won't necessarily know all energy levels, but if you know E2-E1 then you can know that two different spectral lines will differ by this energy.

 

[Philip Land]

You have formulas for the energies of the different levels. The transitions correspond to differences between these energies. If you have states with energies E1, E2 and E3 in ascending order, then in general you expect transitions with energy (E2-E1), (E3-E2) and (E3-E1). You won't necessarily see all in your spectrum and you won't necessarily know all energy levels, but if you know E2-E1 then you can know that two different spectral lines will differ by this energy.

Joining this thread. But since we don't have the finestructure constants the expressions for the energies won't tell us anything. Jut E_1 = A * some number. Will be impossible to solve that set of equations.

How do one identify the lines given the figures above?

 

[mfb]

There are seven numbers or six differences, that should be sufficient to find both unknowns.

 

[mjc123]

This is a fine structure question, not hyperfine, so Eq. 3 is the wrong equation to use. There is no I.