karush
Gold Member
MHB
- 3,240
- 5
$\tiny{45.4.T40}$
Suppose that the coefficient matrix of a consistent system of linear equations has two columns that are identical. Prove that the system has infinitely many solutions. Refer to the DTSLS Diagram
\item using augmented matrix A for example with c1 and c3 identical
$\left[
\begin{array}{rrr|r}
1&4&1&12\\
2&3&2&14\\
3&2&3&16
\end{array}\right]$
eMH returned the following RREF which show c1 and c3 as pivot columns
this is a violation of RREF
$\text{REFF}(A)=\left[ \begin{array}{rrr|r}
1 & 0 & 1 & 4 \\
0 & 1 & 0 & 2 \\
0 & 0 & 0 & 0
\end{array} \right]$
the matrix was dirived from the the possible set of $x_1=1\ x_2=2\ x_3=3$
a little perplexed as to whar we need to do when one row is all zero's after RREF
also as a result of RREF can this be just an 2x4 augmented matrix, r<n
this is supposed to be a proof which I am not good at
here is the DTSLS Diagram we are supposed to us
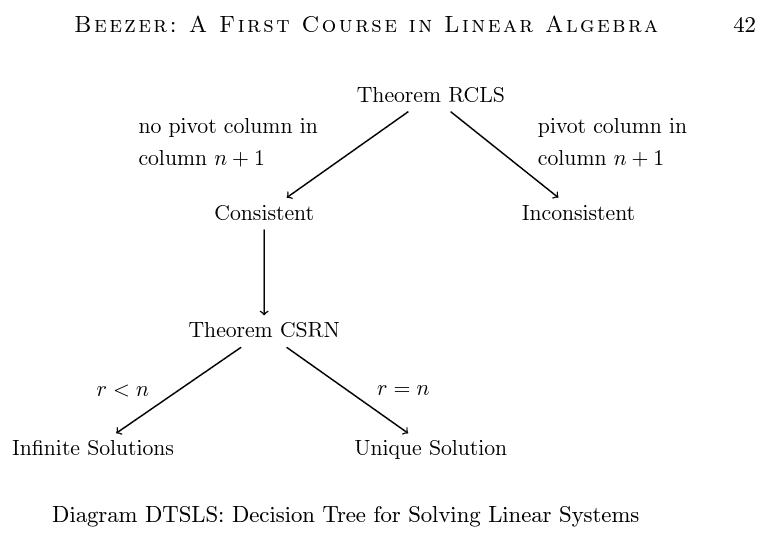
Suppose that the coefficient matrix of a consistent system of linear equations has two columns that are identical. Prove that the system has infinitely many solutions. Refer to the DTSLS Diagram
\item using augmented matrix A for example with c1 and c3 identical
$\left[
\begin{array}{rrr|r}
1&4&1&12\\
2&3&2&14\\
3&2&3&16
\end{array}\right]$
eMH returned the following RREF which show c1 and c3 as pivot columns
this is a violation of RREF
$\text{REFF}(A)=\left[ \begin{array}{rrr|r}
1 & 0 & 1 & 4 \\
0 & 1 & 0 & 2 \\
0 & 0 & 0 & 0
\end{array} \right]$
the matrix was dirived from the the possible set of $x_1=1\ x_2=2\ x_3=3$
a little perplexed as to whar we need to do when one row is all zero's after RREF
also as a result of RREF can this be just an 2x4 augmented matrix, r<n
this is supposed to be a proof which I am not good at
here is the DTSLS Diagram we are supposed to us
Last edited: