SUMMARY
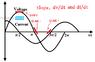
The discussion centers on the behavior of current in an AC capacitive circuit, specifically addressing the phenomenon where current reaches its maximum at the moment when voltage is zero. This occurs because the current through a capacitor is the derivative of the voltage across it, represented by the equation i = C * dV/dt. At the zero crossing of the sine wave voltage (Vc = Vm * sin(ωt)), the slope is steepest, resulting in maximum current flow despite the voltage being zero. The voltage source supplies the energy necessary for the current to flow, challenging the intuitive understanding of energy transfer in capacitive circuits.
PREREQUISITES
- Understanding of AC circuit analysis and sine wave behavior
- Familiarity with capacitive reactance and its role in AC circuits
- Knowledge of the relationship between voltage and current in capacitors
- Basic grasp of calculus, particularly derivatives and their application in electrical engineering
NEXT STEPS
- Study the mathematical principles of sine waves and their derivatives in AC circuits
- Learn about the role of impedance in AC circuits and how it affects current flow
- Explore the concept of resonant LC circuits and energy transfer between inductors and capacitors
- Investigate transient response in RLC circuits and its impact on current and voltage behavior
USEFUL FOR
Electrical engineers, students studying AC circuit theory, and anyone interested in understanding the dynamics of current flow in capacitive circuits.