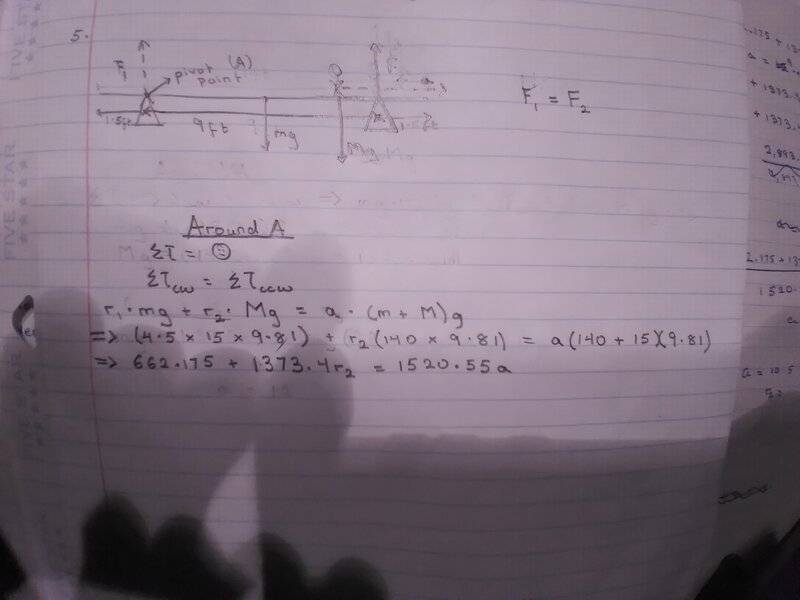SUMMARY
The discussion centers on the confusion surrounding torque equations and the forces acting on a plank supported at two points. Key variables include mg (force of gravity on the plank), Mg (force of a person on the plank), r1 (distance from mg to the pivot), r2 (distance from the person to the pivot), and a (distance the person can walk without tipping the plank). The participants clarify that when analyzing tipping moments, the second support should be considered the pivot point, simplifying the calculations. The correct approach involves balancing counterclockwise and clockwise moments to determine the stability of the system.
PREREQUISITES
- Understanding of basic physics concepts such as torque and moments.
- Familiarity with forces acting on objects in static equilibrium.
- Knowledge of how to calculate moments about a pivot point.
- Ability to interpret and create free-body diagrams.
NEXT STEPS
- Study the principles of static equilibrium in physics.
- Learn how to construct and analyze free-body diagrams.
- Research torque calculations and their applications in real-world scenarios.
- Explore examples of moment balance in engineering problems.
USEFUL FOR
Students and educators in physics, engineers working on structural analysis, and anyone interested in understanding the mechanics of forces and torques in static systems.