Solving Impeller Analysis: 3 Unknowns & 0 Inlet Velocity?

[billy k]

TL;DR

Impeller torque per speed description

Hello there, I am trying to analyze an impeller i found at home (small one) so i can find the torque-speed graph. The thing is that i get stuck in an equation with 3 unknowns instead of 2 and i don't know what else to assume.
My approach is as follows:
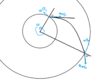
I take the usual equation: $M = \dot{m} ( u_{iφ} R_i - u_{oφ} R_o)$ where M is the torque and i assume that $u_{rel}$ (relative velocity) is tangent to the geometry (see the image). So i substitue: $u_{iφ} = ωR_i - u_{rel,i} cos(25^o) , u_{oφ} = ωR_o - u_{rel,o} cos(21^o)$
and for the mass flow (wich by the way the inlet area and outlet area are equal by geometry) :
$\dot{m} = ρ A_i u_{rel,i} sin(25^o) = ρ A_o u_{rel,o} sin(21^o)$ which gives the relation between the relative speeds (the ω term adds nothing to mass flow).
Therefore i end up with:
$M = [2π R_i b_i u_{rel,i} sin(25^o) ]* [ ω(R_o - R_i) - u_{rel,i} ( cos(25^o) - cos(21^o) * \frac{sin(25^o)}{sin(21^o)} ]$
The last equation has the 3 unknowns and using the Μ-ω of a motor for example i still lack an equation.
Thats my question; what is the third equation? or have i done something wrong so far?
I also want to ask if its realistic to set the inlet velocity to 0 (no whirl at entrance).
Thanks in advance.

 

[jrmichler]

Not to nitpick, but pump torque is heavily dependent on flow in addition to speed. If you really want to do a theoretical analysis of a pump impeller, get a copy of Centrifugal and Axial Flow Pumps, by A. J. Stepanoff. If you don't want to buy it, borrow a copy by interlibrary loan.

I have a copy, I read it, and I convinced myself that I do not ever want to do a theoretical analysis of a pump. Especially since it is so much easier to find the pump curve for a similar pump, then extrapolate using the pump similarity equations.