- #1
Karol
- 1,380
- 22
Homework Statement
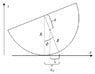
The hemisphere is of radius R.
Prove that the period equals that of a mathematical pendulum of length [itex]4R/3[/itex]
I have a solution, but i don't understand.
Homework Equations
Center of gravity:
[tex]a=\frac{3}{8}R[/tex]
Moment of inertia round the center of mass:
[tex]I_C=\frac{83}{320}mR^2[/tex]
Kinetic energy consists of: T1, linear velocity of center of mass and energy of rotation round center of mass, T2:
[tex]T_1=\frac{1}{2}m \left(\dot{x}^2+\dot{z}^2\right)[/tex]
[tex]T_2=\frac{1}{2}I_C \dot{\phi}^2[/tex]
Potential energy: V=mgz
The Attempt at a Solution
There is no sliding, so, the x coordinate of the center of mass is:
[tex]x_C=\phi R[/tex]
The connection between [itex]\phi[/itex] and x and z:
[tex]x=R \left(\phi -\frac{3}{8}\sin \phi \right)[/tex]
[tex]z=R \left(1-\frac{3}{8}\cos\phi \right)[/tex]
Small angles approximation:
[tex]x=R \frac{3}{8} \phi R [/tex]
[tex]z=R \left( \frac{5}{8} + \frac{3}{16} \phi^2 \right)[/tex]
Now i start not to understand.
It is written that:
[tex]V=\frac{1}{2} \frac{3}{8} mgR \phi^2[/tex]
It has the units of energy, but which?
And:
[tex]T_1=\frac{1}{2} \frac{25}{64} mR^2 \dot{\phi}^2[/tex]
If i compute the members of the kinetic energy, it is only the first member in it.
And the period is:
[tex]\omega^2=\frac{\frac{3}{8} mgR}{\left( \frac{25}{64} + \frac{83}{320} \right) mR^2}[/tex]
The denominator is the moment of inertia round the contact point with the floor.
It resembles the equation for kinetic energy:
[tex]E=\frac{1}{2} I \omega^2[/tex]
But in our solution ω isn't the angular velocity, but the period.