Implementing a weird-looking boundary condition (PDE/FDM)

[maistral]

So I have this problem, taken from Kraus's heat transfer book.

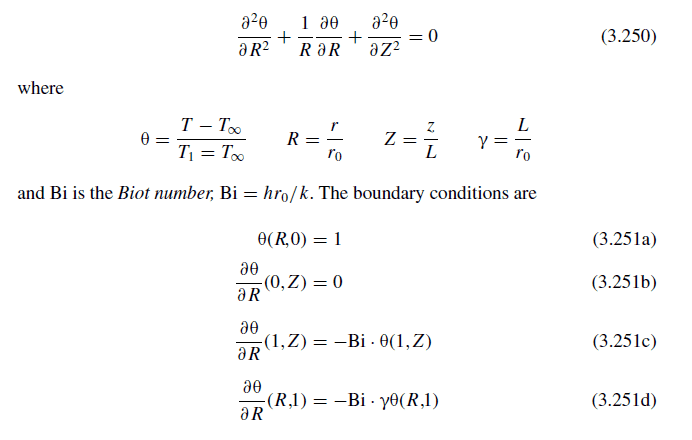
So deriving the computational molecule, the conditions for (3.251a), (3.251b) is a bit of a no brainer. The issue I am having is about the boundaries for (3.251c) and (3.251d). This is actually the first time I have seen this kind of boundary condition.

How do I deal with this? My hypothesis is to integrate the equations (lol) but the constants of integration stay around... I have no idea what to do at all. Bi and γ are constants. Thanks!

 

[maistral]

Oh, to add.

There's an analytical expression for the solution; and I am able to graph the resulting multivariate graph. I intend to do the numerical analysis as another way of solving it. The problem is, even if I implement the 'integrating the boundary condition' part or if I use the ghost point strategy, both of it does not work - the graph from the numerical solution is way too far from the analytical expression's graph.

 

[Chestermiller]

You're solving this by finite difference, correct?

 

[maistral]

Yes sir. Finite difference.

 

[Chestermiller]

$$\theta (1+\Delta R, Z)-\theta (1-\Delta R, Z)=-2(\Delta R) Bi\ \theta (1,Z)$$
so
$$\frac{\partial ^2 \theta}{\partial R^2}=2\frac{(\theta (1-\Delta R, Z)-\theta (1,Z))-(\Delta R) Bi\ \theta (1,Z)}{(\Delta R)^2}$$
or
$$\frac{\partial ^2 \theta}{\partial R^2}=2\frac{(\theta (1-\Delta R, Z)-\theta (1,Z))}{(\Delta R)^2}-2\frac{Bi\ \theta(1,Z)}{\Delta R}$$
or
$$\frac{\partial ^2 \theta}{\partial R^2}=2\frac{(\theta (1-\Delta R, Z)-[1+(\Delta R) Bi]\theta (1,Z))}{(\Delta R)^2}$$

 

[maistral]

Thanks for replying sir. Actually I did it already, but I seem to be getting erroneous results. Could you have my computational molecules for each boundary checked first?

I intend to implement a solution similar to Gauss-Seidel iteration; thus I kept on factoring out the 'center' molecule.

 

[Chestermiller]

Sorry. I'll help with the finite differencing, but, as far as the debugging is concerned, you're on your own.

 

[maistral]

Oh, it's alright sir.

Apparently my computational molecules for the boundaries are correct; but the numerical solution is still given different values. I'm starting to think that the problem comes from the corners - problem is what should I do with the corners (0,1) and (1,1). What boundary should I invoke? Say for the upper left corner (0,1); is it 3.251b or 3.251d?

 

[Chestermiller]

Oh, it's alright sir.

Apparently my computational molecules for the boundaries are correct; but the numerical solution is still given different values. I'm starting to think that the problem comes from the corners - problem is what should I do with the corners (0,1) and (1,1). What boundary should I invoke? Say for the upper left corner (0,1); is it 3.251b or 3.251d?

Both