DanielMB
- 24
- 12
- TL;DR
- Relationship among implication, Boolean expression and Venn diagrams
Hello, I’m having difficulties understanding logical relations “A implies B” and “A if and only if” using Boolean expressions and Venn diagrams, there is something where I’m wrong, but I could not find it out. Please, be benevolent and tell me where I’m wrong. Thanks
Note : Obviously I’m supposing that A,B are not null sets
A implies B
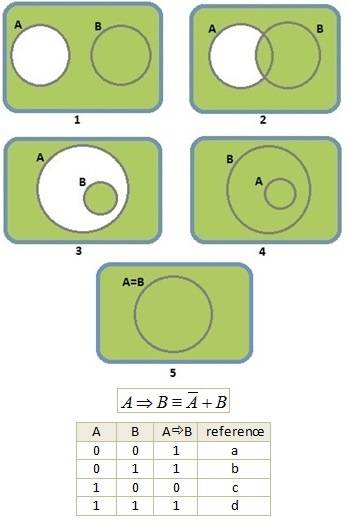
Representing “A implies B” using Boolean expression as “–A+B” and the correlated Venn diagrams, knowing that the truth table for “A implies B” is (see attached image)
“A implies B” can be represented by the following Venn diagrams, all of them acomplishing “-A+B” expression (see attached image)
But I’ve found that those diagrams (Vn) are not full compatible with the corresponding truth table
Should I discard (V1, V3, V5)? Are there additional hypotheses?, like the following
A if and only if B
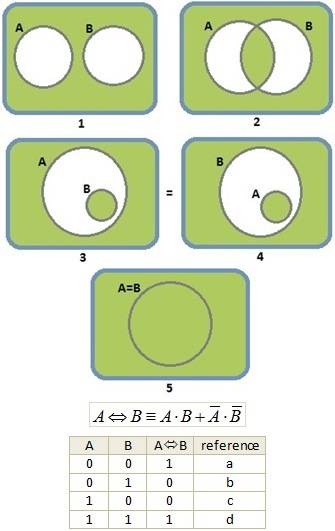
Representing “A if and only if B” using Boolean expression as “(A.B)+(-A.-B)” and the correlated Venn diagrams, knowing that the truth table for “A if and only if B” is (see attached image)
“A if and only if B” can be represented by the following Venn diagrams, all of them acomplishing “(A.B)+(-A.-B)” expression (see attached image)
Note : V3 and V4 are equivalent, because “A if and only if” is conmutative
But I’ve found that those diagrams (Vn) are not full compatible with the corresponding truth table
Should I discard (V1)? Are there additional hypotheses?, like the following
Thanks
Note : Obviously I’m supposing that A,B are not null sets
A implies B
Representing “A implies B” using Boolean expression as “–A+B” and the correlated Venn diagrams, knowing that the truth table for “A implies B” is (see attached image)
“A implies B” can be represented by the following Venn diagrams, all of them acomplishing “-A+B” expression (see attached image)
But I’ve found that those diagrams (Vn) are not full compatible with the corresponding truth table
V1: a, b, -c, -d -> Not according to truth table
V2: a, b, -c, d -> According to truth table
V3: a, -b, -c, d -> Not according to truth table (but according to “A if and only if B” truth table)
V4: a, b, -c, d -> According to truth table
V5: a, -b, -c, d -> Not according to truth table (but according to “A if and only if B” truth table)
Should I discard (V1, V3, V5)? Are there additional hypotheses?, like the following
H1) A, B with not null intersection : to reject V1
H2) B is not an A subset : to reject V3
H3) A not equal to B : to reject V5
A if and only if B
Representing “A if and only if B” using Boolean expression as “(A.B)+(-A.-B)” and the correlated Venn diagrams, knowing that the truth table for “A if and only if B” is (see attached image)
“A if and only if B” can be represented by the following Venn diagrams, all of them acomplishing “(A.B)+(-A.-B)” expression (see attached image)
Note : V3 and V4 are equivalent, because “A if and only if” is conmutative
But I’ve found that those diagrams (Vn) are not full compatible with the corresponding truth table
V1: a, -b, -c, -d -> Not according to truth table
V2: a, -b, -c, d -> According to truth table
V3: a, -b, -c, d -> According to truth table
V4: a, -b, -c, d -> According to truth table
V5: a, -b, -c, d -> According to truth table
Should I discard (V1)? Are there additional hypotheses?, like the following
H1) A, B with not null intersection : to reject V1
Thanks