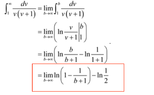Improper integral from 1 to infinity

In summary, an improper integral from 1 to infinity is evaluated over an unbounded interval and is undefined in the traditional sense. It is evaluated by taking the limit as the upper limit of integration approaches infinity, and is convergent if the limit exists and is a finite number. This type of integral has important applications in calculus and can have a negative value if the function being integrated has negative values over the interval.
  • #1
yeny
7
0
View attachment 8443

Hello everyone,

I am stuck on this homework problem. I got up to (ln (b / (b+1) - ln 1 / (1+1) ) but I'm not sure how to go to the red boxed step where they have (1 - 1 / (b+1) )

if anyone can figure it out Id really appreciate it.

thank you very much.
 

Attachments

  • Screen Shot 2018-09-24 at 5.30.31 PM.png
    Screen Shot 2018-09-24 at 5.30.31 PM.png
    38.8 KB · Views: 78
Physics news on Phys.org
  • #2
$\frac{b}{b+1} = \frac{b+1-1}{b+1} = \frac{b+1}{b+1} + \frac{-1}{b+1} = 1 - \frac{1}{b+1}$
 
  • #3
THANK YOU soo much for your help and time. Really appreciate it!
 

FAQ: Improper integral from 1 to infinity

What is an improper integral from 1 to infinity?

An improper integral from 1 to infinity is a type of integral that is evaluated over an unbounded interval, such as from 1 to infinity. This means that the upper limit of integration is not a finite number, which makes the integral undefined in the traditional sense.

How is an improper integral from 1 to infinity evaluated?

An improper integral from 1 to infinity is evaluated by taking the limit as the upper limit of integration approaches infinity. This means that the integral is evaluated as a definite integral with a variable upper limit, and then the limit is taken to determine the final value.

When is an improper integral from 1 to infinity convergent?

An improper integral from 1 to infinity is convergent if the limit of the integral exists and is a finite number. This means that the integral can be evaluated and has a well-defined value, despite having an unbounded interval of integration.

What is the significance of an improper integral from 1 to infinity in mathematics?

An improper integral from 1 to infinity has important applications in calculus, particularly in the study of functions and their behavior over unbounded intervals. It allows for the evaluation of integrals that would otherwise be undefined, and is essential for understanding the concept of convergence.

Can an improper integral from 1 to infinity have a negative value?

Yes, it is possible for an improper integral from 1 to infinity to have a negative value. This occurs when the function being integrated has negative values over the interval of integration, and the area under the curve below the x-axis is greater than the area above the x-axis.

Similar threads

MHB Improper integral of an even function
Replies
2
Views
2K
I Integrating 1/x with units (logarithm)
Replies
15
Views
2K
MHB Improper integral convergence/divergence
Replies
5
Views
2K
I Unsure of solution to improper integral
Replies
3
Views
1K
MHB Improper integral and L'Hôpital's rule
Replies
1
Views
2K
MHB Can the Series Sum Be Expressed as an Integral as N Approaches Infinity?
Replies
3
Views
1K
I Troubleshooting a difficult integral
Replies
6
Views
2K
B Calculating shaded area: I'm getting discrepancies between methods
Replies
3
Views
2K
MHB How Does Integration to Infinity Work in Calculus?
Replies
2
Views
1K
Improper integral, infinite limits of integration
Replies
7
Views
2K

Hot Threads

Recent Insights

Back
Top