In Euclidian space, closed ball is equal to closure of open ball

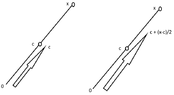
[CGandC]

Problem: Let $(X,d)$ be a metric space, denote as $B(c,r) = \{ x \in X : d(c,x) < r \}$ the open ball at radius $r>0$ around $c \in X$, denote as $\bar{B}(c, r) = \{ x \in X : d(c,x) \leq r \}$ the closed ball and for all $A \subset X$ we'll denote as $cl(A)$ the closure of $A$ ( sometimes denoted also as $\bar{A}$ ).

Show that in $\mathbb{R}^n$ with the standard metric it occurs that: $cl(B(c, r))=\bar{B}(c, r)$

Attempt:
$( \subseteq )$ Let $\tau \in cl(B(c,r))$. There exists a sequence $x_n \in B(c,r)$ s.t. $x_n \rightarrow \tau$
( From a theorem that says: $x \in cl(B) \iff$ there exists a sequence $x_n \in B$ , $x_n \rightarrow x$ ).
Note that for all $n \in \mathbb{N}$, from the fact $x_n \in B(c,r)$ we have $d(c,x_n) < r$. Also, since $x_n \rightarrow \tau$ we have that $d(x_n,\tau) \rightarrow 0$.
So by triangle inequality, we have for all $n \in \mathbb{N}$ that $d(c,x) \leq d(c,x_n) + d(x,x_n)$, taking the limit we get $d(c,x) \leq r$.

$( \supseteq )$ Let $\tau \in \bar{B}(c,r)$, hence $d(c,\tau) \leq r$.
( Now we want to show that $\tau \in cl(B(c,r))$, meaning for all $r>0$ we want to show $B(\tau,r) \cap B(c,r) \neq \emptyset$ )
Let $r>0$. Notice that $\tau \in B(\tau,r)$ since $d(\tau,\tau) =0 < r$. In addition we have $\tau \in \bar{B}(c,r)$ then $d(\tau,c) \leq r$.
If $d(\tau,c)<r$ then $\tau \in B(c,r)$,
hence $\tau \in B(\tau,r) \cap B(c,r)$.
If $d(\tau,c) = r$ then [ missing arguments for completing proof ].How to prove the "$( \supseteq )$" side? I thought maybe I'd use the theorem "$x \in cl(B) \iff$ there exists a sequence $x_n \in B$ , $x_n \rightarrow x$ "; that means I'd show the existence of a sequence $(x_k)_{k=1} \subseteq R^n$ s.t. $(x_k)_{k=1} = ((x^{(1)}_i)_{i=1}^n,(x^{(2)}_i)_{i=1}^n,... )$ s.t. $x_k = (x^{(k)}_i)_{i=1}^n$ s.t. $(x^{(k)}_i)_{i=1}^n \in R^n$ , but the question is how to define this sequence of sequences?

 

[andrewkirk]

You don't need a sequence of sequences.
For a point $x$ on the boundary of the closed ball, why not just approach it by the sequence that goes along the line segment from $c$ to $x$, starting at $c$ and at each step jumping to halfway between current location and $x$. You should be able to prove that converges to $x$ and that all its points are in the open ball.

 

[CGandC]

Ok, here's what I've did:
I started drawing an intuitive ( non-precise ) picture of what you've said,

I've noted that In the attempted proof I gave I had mistaken with the arbitrary $r$ I introduced with the $r$ given in the question. Here's my attempted proof based on your idea:


Let $\tau \in cl(B(c,r))$ be arbitrary. Hence $d(c,\tau) \leq r$.
Take the sequence $(x_m) \subseteq \mathbb{R}^n$ defined as follows,
For every $m \in \mathbb{N}$, $x_m = c + \sum_{k=1}^{m}\frac{\tau-c}{2^i} = c + \frac{1}{2}\cdot(\tau-c)\sum_{k=0}^{m-1} \frac{1}{2^k} = c + ( \tau - c)\cdot(1-(\frac{1}{2})^m)$
Note that $\lim_{m\to\infty}x_m = \tau$.
Also note that $x_m$ is a vector equation, meaning that for all $1 \leq i \leq n$ , $(x_m)_i = c_i + ( \tau_i - c_i)\cdot(1-(\frac{1}{2})^m)$, from this, note that $(x_m) \subseteq B(c,r)$ since for all $m \in \mathbb{N}$ we have that $d(c,x_m) = \sqrt{ \Bigg( c_1 - \bigg( c_1 + ( \tau_1 - c_1)\cdot(1-(\frac{1}{2})^m) \bigg) \Bigg)^2 + \cdots + \Bigg( c_n - \bigg( c_n + ( \tau_n - c_n)\cdot(1-(\frac{1}{2})^m) \bigg) \Bigg)^2 } = ( 1 - (\frac{1}{2})^m ) \sqrt{ ( \tau_1 - c_1)^2 + \cdots + ( \tau_n - c_n)^2 }.$ Since $d(c,\tau) \leq r$ we can see that $d(c,x_m) < r$, hence $(x_m) \subseteq B(c,r)$. So since $\lim_{m\to\infty}x_m = \tau$ and $\tau$ was arbitrary, we're finished.Do you think this is ok?

 

[wrobel]

Sometimes a general fact is much easier to prove because the key points are presented explicitly.

Let $f:X\to \mathbb{R}$ be a convex continuous function on the normed vector space $X$. Then
$$\mathrm{cl}\,\{x\in X\mid f(x)<c\}=\{x\in X\mid f(x)\le c\}$$

 

[CGandC]

Thanks but I haven't learned about convex functions and normed vector spaces yet (I'm doing a real analysis course and just very little of the basics of topology are taught). It seems to me that If I can create such a function as you've said, the proof will be finished.

 

[wrobel]

Convex function is a function such that the inequality
$$f(\lambda x_1+(1-\lambda)x_2)\le \lambda f(x_1)+(1-\lambda)f(x_2)$$
holds for all $$x_1,x_2\in X,\quad \lambda\in[0,1].$$
Take $f(x)=\|\tilde x-x\|$ and $X=\mathbb{R}^m$

 

[andrewkirk]

@CGandC Yes your proof works.

 

[CGandC]

Convex function is a function such that the inequality
$$f(\lambda x_1+(1-\lambda)x_2)\le \lambda f(x_1)+(1-\lambda)f(x_2)$$
holds for all $$x_1,x_2\in X,\quad \lambda\in[0,1].$$
Take $f(x)=\|\tilde x-x\|$ and $X=\mathbb{R}^m$

Ok now I understand how the general theorem you proposed relates to the problem. In the private case you proposed I get what I'm asked to prove. How do I prove the "$\supseteq$" direction? got a hint please?

Here's what I've done ( had no clue how to proceed beyond the beginning ):
Let $x$ be arbitrary such that $f(x) \leq c$. Let $r>0$. We'll show that $B(x,r) \subseteq \{ y \in X : f(y) < c \}$. Let $\tau \in B(x,r)$, thus $d(x,\tau)<r$. [ I don't see how can I relate $\tau$ to $f$ in order to have $f(\tau) < c$. ]

I then thought maybe I'd find a sequence $x_n \in \{ y \in X : f(y) < c \}$ which converges to $x$ and that'd show $x$ is in $\mathrm{cl}\,\{x\in X\mid f(x)<c\}$ , but couldn't think of anything that'd help me allow to do that.

@CGandC Yes your proof works.

Thanks for the help!