In the Stern Gerlach experiment, electron beam acceleration question

[mesa]

In the Stern Gerlach experiment it would seem that an electron beam moving at some velocity bisecting the upper magnet on a horizontal path would be radially accelerated perpendicular to the direction of motion.

I am assuming from Lenz's Law this can be corrected by increasing the B_f depending on the position and direction that the electron beam is fired into the experiment, here are two scenarios:

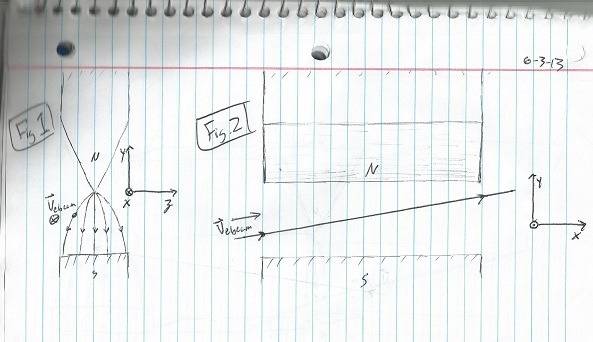
Figure 1 shows an electron beam fired horizontally along the positive x-axis slightly off center from the bisection of the experiment. As the beam is radially accelerated in the positive z direction the magnetic field increases counteracting this effect although it would seem there would still be some bending along the z axis.

Figure 2 is a representation of our beam now fired along the positive y/z plane bisecting our experiment. As the beam travels upward the B_f increases canceling the radial acceleration. This would seem like a more reasonable way to control the electron beam.

Is either of these two scenarios correct? some combination of the two? or am I just way out in left field?

 

[mfb]

I don't see the issue.
If you want to use an electron beam, you can use an electric field to cancel the force in z-direction. The magnetic field will always give a force in the same direction, changing its magnitude does not help.
Even if you don't use an electric field: so what? The interesting deflection happens in y-direction.

 

[mesa]

I don't see the issue.
If you want to use an electron beam, you can use an electric field to cancel the force in z-direction. The magnetic field will always give a force in the same direction, changing its magnitude does not help.

I am looking at the experiment from the standpoint of R=mv/qB_f causing a radial acceleration perpendicular to that of motion from the two permanent magnets (like in a mass spectrometer).

I figured the only way to adjust for this acceleration is through Lenz's Law by increasing the B_f by altering the direction of the beam through the gradient of the field. It seems what you are saying is the experiment uses an external E_f that counteracts this acceleration as opposed to taking advantage of Lenz's Law, is that right?

Even if you don't use an electric field: so what? The interesting deflection happens in y-direction.

No doubt, I just want to make sure I understand the idiosyncrasies before getting into the good stuff.

 

[mfb]

I am looking at the experiment from the standpoint of R=mv/qB_f causing a radial acceleration perpendicular to that of motion from the two permanent magnets (like in a mass spectrometer).

Why?

I figured the only way to adjust for this acceleration is through Lenz's Law by increasing the B_f by altering the direction of the beam through the gradient of the field.

You would have to reverse the field polarity for that. And that is really bad for the main experiment.

It seems what you are saying is the experiment uses an external E_f that counteracts this acceleration as opposed to taking advantage of Lenz's Law, is that right?

That is possible.

 

[mesa]

Why?

Without either an external E_f/B_f or enough of a change in ∅_m the electron beam would move out of the experiment due to radial acceleration perpendicular to the velocity of the beam. I think it is important to know how this acceleration is compensated for so I can better understand the experiment before diving into QM.

The Stern Gerlach experiment is the proverbial 'line in the sand' that separated classical/relativistic mechanics from QM setting the stage for an entirely new realm of physics is it not? I would imagine understanding this experiment, it's implications and everything about it is important to gaining a greater understanding of QM in the future. I am very excited about the prospect.

You would have to reverse the field polarity for that. And that is really bad for the main experiment.

I don't understand why the field polarity would need to be reversed, wouldn't a large enough increase in ∅_m be able to counteract the radial acceleration or is there something beyond Faraday and Lenz that I have yet to learn? If so please elaborate.

 

[Fightfish]

Without either an external E_f/B_f or enough of a change in ∅_m the electron beam would move out of the experiment due to radial acceleration perpendicular to the velocity of the beam. I think it is important to know how this acceleration is compensated for so I can better understand the experiment before diving into QM.

Well, the answer is actually very simple - don't use electron beams! In their original experiment, Stern and Gerlach used silver atoms. When you use electrons, there is even additional doubt cast upon the validity of using the classical equations of motion to describe their trajectories.
With silver atoms, most of your problems are solved, and then you can "dive into QM" and leave the electron problems to another time.

 

[vanhees71]

This is a quantum experiment anyway and should be treated quantum-mechanically. It's not very difficult (at least when using the usual approximations). A very nice treatment can be found in the paper

G. Potel, F. Barranco, S. Cruz-Barrios, and J. Gómez-Camacho, Quantum mechanical description of Stern-Gerlach experiments, Phys. Rev. A 71, 052106 (2005).
http://arxiv.org/abs/quant-ph/0409206

 

[Meir Achuz]

Electrons are not usually usd in the S-G experiment, because there is a spread in their deflection due to evXB deflection, that wipes out the magnetic moment deflection difference.
This is explained in Mott and Massey, "Theory of Atomic Collisions", but I think it has been forgotten by later books.

 

[mesa]

Well, the answer is actually very simple - don't use electron beams! In their original experiment, Stern and Gerlach used silver atoms. When you use electrons, there is even additional doubt cast upon the validity of using the classical equations of motion to describe their trajectories.
With silver atoms, most of your problems are solved, and then you can "dive into QM" and leave the electron problems to another time.

I have read about the original experiment, silver was the best option they came up with at the time but it is a complex atom. There have been experiments using electron beams as well. Since this is an elementary particle I thought it would make it easier to model than something with 47 protons and electrons although it seems that the consensus is since it is neutral this would be a better approach.

What do you mean by, "...even additional doubt cast upon the validity of using classical equations of motion to describe trajectories"? Do charged particles moving at some velocity through a B_f not behave as predicted by classical mechanics? Or are you referring to the trajectories of the electrons exiting the experiment and impacting the screen?

This is a quantum experiment anyway and should be treated quantum-mechanically. It's not very difficult (at least when using the usual approximations). A very nice treatment can be found in the paper

G. Potel, F. Barranco, S. Cruz-Barrios, and J. Gómez-Camacho, Quantum mechanical description of Stern-Gerlach experiments, Phys. Rev. A 71, 052106 (2005).
http://arxiv.org/abs/quant-ph/0409206

I went to your link but can not view that paper with my account, any chance you have some other place to view this?

On the other part of your post, I thought the quantum mechanical description dealt with the properties of the individual particles and classical mechanics still applied as far as describing the motion of charged particles moving through magnetic fields. I just want to see how the particles are moved through the experiment. I didn't think an understanding of QM was necessary for this, is that not the case?

Electrons are not usually usd in the S-G experiment, because there is a spread in their deflection due to evXB deflection, that wipes out the magnetic moment deflection difference.
This is explained in Mott and Massey, "Theory of Atomic Collisions", but I think it has been forgotten by later books.

So if the electron beam is subjected to an increasing B_f by having the beam shot as shown in Figure 2 to counteract the evXB deflection this will 'wipe out' the magnetic moment of the electron? That is interesting, to make sure I understand what you are saying, by doing this the electron's behavior changes and will now act as predicted classically? Or does the pattern impacting the screen not resemble anything we would expect?

Or do you mean the magnetic field generated by the motion of the individual electrons interacting with others around it 'upsets' the final trajectory?

 

[vanhees71]

The link to the arXiv should work. There you can download the paper for free from any internet connection.

You can treat the motion of charged particles in the static electromagnetic field approximately by the classical equations of motion, at least in the usual approximations, where the force is a linear function of the space coordinates. That's due to Ehrenfest's theorem, according to which in this case the center of Schrödinger wavepackets move like the classical particles.

As far as I know, there's no SG experiment with charged particles, because then the Lorentz force $q \vec{v} \times \vec{B}/c$ disturbs the splitting according to the magnetic moment (spin).

The most precise modern SG experiments I'm aware of are done with neutrons, which are electrically neutral and have spin 1/2.

For the purpose of the principle of the experiment the original method with atoms is precise enough.

A funny detail is that the original experiment, undertaken in 1923, proved a wrong model, namely Bohrs atom model, which predicted also the splitting into two beams (not 3 as one would expect by the assumptions make about the spin, which was thought to be 1 rather then 1/2) by the same amount as the modern theory predicts, because at the time nobody knew about spin 1/2 and the gyro-factor 2 for electrons, which is in fact a prediction of Dirac's wave equation (or tree-level QED).

That the experiment worked at all was also a lucky event and was due to Gerlach's love for cheap cigars: The cigar smoke contained enough sulfur to lead to a better contrast when developing the photoplates irradiated by the silver-atom beams. Nowadays, where smoking is strictly forbidden on the entire Frankfurt university, the experiment wouldn't work in the original setup, at least not as well as when Stern and Gerlach smoked enough in their lab ;-)).

 

[mesa]

The link to the arXiv should work. There you can download the paper for free from any internet connection.

Yes, it is working now. Although I do not know qm yet it is interesting that the particles fired through the experiment exhibit focusing/de-focusing if they deviate from a horizontal path through the experiment. Is this caused by changing magnetic flux acting on the charges within the atoms?

You can treat the motion of charged particles in the static electromagnetic field approximately by the classical equations of motion, at least in the usual approximations, where the force is a linear function of the space coordinates. That's due to Ehrenfest's theorem, according to which in this case the center of Schrödinger wavepackets move like the classical particles.

So to make sure I understand, a classical approach to moving charges in static magnetic fields and through changing magnetic flux is usually okay but when we get into individual 'wavepackets' and/or non-uniform Forces these rules no longer apply.

As far as I know, there's no SG experiment with charged particles, because then the Lorentz force $q \vec{v} \times \vec{B}/c$ disturbs the splitting according to the magnetic moment (spin).

The most precise modern SG experiments I'm aware of are done with neutrons, which are electrically neutral and have spin 1/2.

I could be wrong about electron beams in SG experiment. After some looking I came across this:
http://digitalcommons.unl.edu/cgi/viewcontent.cgi?article=1031&context=physicsgay

A funny detail is that the original experiment, undertaken in 1923, proved a wrong model, namely Bohrs atom model, which predicted also the splitting into two beams (not 3 as one would expect by the assumptions make about the spin, which was thought to be 1 rather then 1/2) by the same amount as the modern theory predicts, because at the time nobody knew about spin 1/2 and the gyro-factor 2 for electrons, which is in fact a prediction of Dirac's wave equation (or tree-level QED).

I had read about that in an article published on the Stanford site. I believe it was titled, "Right Experiment, Wrong Theory" or something to that effect.

That the experiment worked at all was also a lucky event and was due to Gerlach's love for cheap cigars: The cigar smoke contained enough sulfur to lead to a better contrast when developing the photoplates irradiated by the silver-atom beams. Nowadays, where smoking is strictly forbidden on the entire Frankfurt university, the experiment wouldn't work in the original setup, at least not as well as when Stern and Gerlach smoked enough in their lab ;-)).

Hah ha ha! That is fantastic!