How can I solve this physics problem step by step?

[Frouel]

Homework Statement

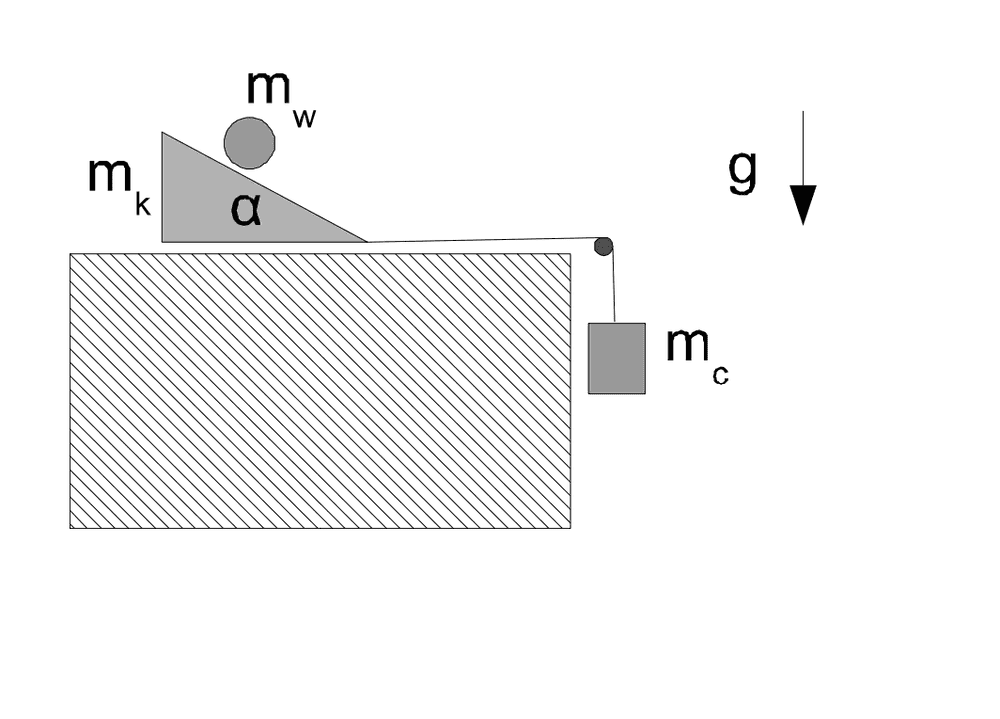
Consider the layout shown in the figure. ˙
A roller with a mass m_w and radius and moment inertia about the axis of rotational symmetry
I = ((m_w)R^2)/2 rolls without slippage and without rolling friction on an inclined plane (with an angle of inclination α) parts of the block, and the block of mass m_k moves without friction on the stationary table. The mass of the weight is m_c.
a) for the data m_k, m_c, R, α determine the mass of the cylinder
m_w, at which the cylinder can rest relative
block demo;
b) for the data m_w, m_k, R, α, determine the mass of the mass m_c at which the block may rest
to the table;
c) for (any) data m_k, R, m_w, α and
block acceleration a_k find the mass of the weight
m_c.
The acceleration due to gravity is g

Relevant Equations

a = gsina.
I = ((m_w)R^2)/2
a = m_c*g/(m_c+m_k+m_w)

I attended to many attemps and I not able to find out no dependencies in this layout. Does someone can show me how to solve this problem step by step? What we must take into considarion in solving such tasks?. How to start?. I got stuck.
This task is from Polish Physics Olympics.

 

[kuruman]

I don't think you will find (m)any people here willing to show you how to solve this step by step because it is against forum rules. Please read them. Nevertheless, I will tell you where I would start. I would forget the hanging mass and find how much force is needed to push on the incline so that the roller is at rest relative to it. Then I would consider that this force comes from the tension in the string.

Also, please be considerate to those who read your posts. Although you fulfilled the letter of the law and posted your attempt, it is very difficult to decipher what you did. I have no doubt that if you submitted this to the Olympics referees, it would not get much traction. I strongly recommend that you use LaTeX (click on "LaTeX guide" above "Attach files") on the lower left to see how it is done. I also recommend that you specify with words what all the variables that you use stand for.

 

[haruspex]

Your equation starting $\sin(\alpha)=$ is dimensionally incorrect. You forgot to square root. But you'd do better to work with tan, not sin.

Further to @kuruman's comments and advice...
It is going to be tough commenting on specific sections of your work. Per forum rules, images are for diagrams and textbook extracts. Your working should be typed in. If you must post images of algebra, number every equation.

It also helps to include some explanation of how you get your equations, e.g. "horizontal forces and acceleration of ... in the reference frame of ...".