- #1
calzone41
- 6
- 0
Thread moved from the technical forums to the schoolwork forums
TL;DR Summary: Struggling to structure the problem and derive an analytical solution for gas expanding into other gas in a rigid tank. Preferred formulation is fixed control volumes. This is not a homework problem.
The problem:
Two control volumes (A and B) are in a rigid tank filled with air. The initial state of each control volume is completely defined. There is a pressure differential between the control volumes so mass flows from A to B. Mass flows such that the pressure in each control volume is equal at time 2. There is no energy transfer or work to or from the tank; frictional losses are ignored. Mass and energy are conserved. There is no heat transfer between air masses except for mass transfer across the control volume boundary. Assume immediate and perfect mixing as mass moves into control volume B. I need to be able to calculate the final state of the air masses in the control volumes (P, m, T). This is straightforward to do numerically, I would like an analytical solution.

Some Background:
This is not a homework assignment. Ultimately I am trying to build a discrete-time-step Stirling engine simulator that models each air mass separately (imagine a gamma configuration engine with hot and cold air masses in a displacer cylinder and a power air mass in a power cylinder.) At each time step, various air masses gain/lose energy and perform work, so will have different pressures. I need to balance these pressures at the end of each time step. Eventually, I will be modeling three connected air masses, but wanted to understand the two-airmass problem first before adding complexity.
Attempted solutions
Systems of Equations:
Using fixed-size control volumes, there are 5 unknowns at the final state (mA, mB, TA, TB, P2). I find 4 equations: conservation of mass, conservation of enthalpy ( that is; hA1mA1 + hB1mB1 = hA2mA2 + hB2mB2. Is this a valid equation?), and ideal gas law for both volumes at the end state. This would not be enough to solve for 5 unknowns. Is there another obvious one? I considered relationships for polytropic processes, but was not confident they apply for fixed control volumes. I did derive a 5th equation that relates internal energy to mass flow for control volume A (shown below) but I'm hesitant about it. Solving this non linear system of equations is beyond me. Perhaps you can point me in the right direction?
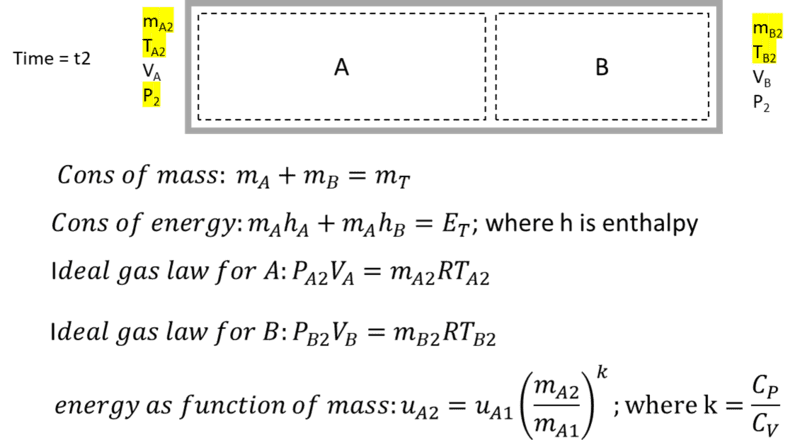
Control volume energy balance, integral with respect to time:
Starting with the general energy balance equation for volume A, I eliminated terms for heat flux, work, and mass flow in. I then differentiated (chain rule) um with respect to t. The m-dot term here makes no physical sense (mass does not just disappear) so is zero. Using the definition of enthalpy, the ideal gas law, the specific heat relationship u = CvT, the definition of k = Cp/Cv, and integrating both sides of this separable differential equation. I arrive at internal energy as a function of mass flow and time. assuming mass flow is constant this can be re-written as internal energy as a function of mass in the control volume. (Note: It is possible to perform this integration as du/dm rather than du/dt. The result is the same.) This is an simple, elegant equation (which I cannot verify externally). However, when using this relationship to assemble a differential equation for control volume B, I get an unwieldy equation I cannot figure out how to integrate.
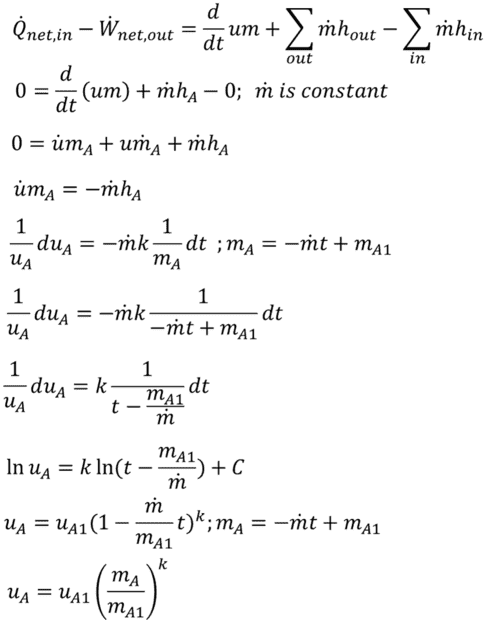
Combined control mass and control volume:
I can also structure the problem as control masses instead of control volumes. Essentially, mass A pushes into mass B, doing work Imagine a piston between the air masses. Using polytropic relationships for isentropic flow, and the relationship of total volume being constant, I can solve for P2. I can then use this P2 and the control volume relationships to solve for the changes in mass, then find other equations of state. This is fine, but feels messy and kludged.
Questions:
Am I making this problem more complicated than it needs to be? Is there a simpler way to solve the problem of gas expanding into other gas in a rigid tank?
Side question: Is conservation of enthalpy a thing? When using this relationship I can get an equation for P2 that is essentially an arithmetic mean [P2 - (Pa1Va + Pb1Vb)/(Va + Vb)], which differs from the P2 found using control masses and polytropic relationships and seems too simple to be real.
Any help in how to think about this problem would be appreciated. Thanks in advance!
The problem:
Two control volumes (A and B) are in a rigid tank filled with air. The initial state of each control volume is completely defined. There is a pressure differential between the control volumes so mass flows from A to B. Mass flows such that the pressure in each control volume is equal at time 2. There is no energy transfer or work to or from the tank; frictional losses are ignored. Mass and energy are conserved. There is no heat transfer between air masses except for mass transfer across the control volume boundary. Assume immediate and perfect mixing as mass moves into control volume B. I need to be able to calculate the final state of the air masses in the control volumes (P, m, T). This is straightforward to do numerically, I would like an analytical solution.
Some Background:
This is not a homework assignment. Ultimately I am trying to build a discrete-time-step Stirling engine simulator that models each air mass separately (imagine a gamma configuration engine with hot and cold air masses in a displacer cylinder and a power air mass in a power cylinder.) At each time step, various air masses gain/lose energy and perform work, so will have different pressures. I need to balance these pressures at the end of each time step. Eventually, I will be modeling three connected air masses, but wanted to understand the two-airmass problem first before adding complexity.
Attempted solutions
Systems of Equations:
Using fixed-size control volumes, there are 5 unknowns at the final state (mA, mB, TA, TB, P2). I find 4 equations: conservation of mass, conservation of enthalpy ( that is; hA1mA1 + hB1mB1 = hA2mA2 + hB2mB2. Is this a valid equation?), and ideal gas law for both volumes at the end state. This would not be enough to solve for 5 unknowns. Is there another obvious one? I considered relationships for polytropic processes, but was not confident they apply for fixed control volumes. I did derive a 5th equation that relates internal energy to mass flow for control volume A (shown below) but I'm hesitant about it. Solving this non linear system of equations is beyond me. Perhaps you can point me in the right direction?
Control volume energy balance, integral with respect to time:
Starting with the general energy balance equation for volume A, I eliminated terms for heat flux, work, and mass flow in. I then differentiated (chain rule) um with respect to t. The m-dot term here makes no physical sense (mass does not just disappear) so is zero. Using the definition of enthalpy, the ideal gas law, the specific heat relationship u = CvT, the definition of k = Cp/Cv, and integrating both sides of this separable differential equation. I arrive at internal energy as a function of mass flow and time. assuming mass flow is constant this can be re-written as internal energy as a function of mass in the control volume. (Note: It is possible to perform this integration as du/dm rather than du/dt. The result is the same.) This is an simple, elegant equation (which I cannot verify externally). However, when using this relationship to assemble a differential equation for control volume B, I get an unwieldy equation I cannot figure out how to integrate.
Combined control mass and control volume:
I can also structure the problem as control masses instead of control volumes. Essentially, mass A pushes into mass B, doing work Imagine a piston between the air masses. Using polytropic relationships for isentropic flow, and the relationship of total volume being constant, I can solve for P2. I can then use this P2 and the control volume relationships to solve for the changes in mass, then find other equations of state. This is fine, but feels messy and kludged.
Questions:
Am I making this problem more complicated than it needs to be? Is there a simpler way to solve the problem of gas expanding into other gas in a rigid tank?
Side question: Is conservation of enthalpy a thing? When using this relationship I can get an equation for P2 that is essentially an arithmetic mean [P2 - (Pa1Va + Pb1Vb)/(Va + Vb)], which differs from the P2 found using control masses and polytropic relationships and seems too simple to be real.
Any help in how to think about this problem would be appreciated. Thanks in advance!