FranzDiCoccio
- 350
- 43
- Homework Statement
- A skier starts from rest at the top of a hill. The skier coasts down the hill and up a second hill, as the drawing illustrates. The crest of the second hill is circular, with a radius of r = 36 m. Neglect friction and air resistance. What must be the height h of the first hill so that the skier just loses contact with the snow at the crest of the second hill?
- Relevant Equations
- conservation of mechanical energy
Newton's second law
This is problem 49 in chapter 6 of "Physics - 9th edition". A similar question was asked here several years ago (although with a different height).
The figure is below. I added point A and angle \theta.
The solution is pretty easy. For the purpose of my discussion I'm assuming that the height is zero at the "center" of the rightmost hill, and consider a generic point A on such hill, instead of its crest. The radius going through A forms an angle \theta with the vertical direction. The answer to the question can be obtained by setting \theta =0 in the solution.
The condition for losing contact at A is that the normal force there is null, which means that the centrifugal force equals the projection of the weight along the radial direction. This gives v^2 = g r \cos \theta.
Conservation of total mechanical energy requires that 2 g h_0 =2 g r \cos \theta + v^2, where h_0 is the height of the leftmost hill wrt the center of the leftmost hill. Substituting the first equation into the second one we get
h_0 = \frac{3}{2} r \cos \theta
Since the height of point A is r \cos \theta, the starting point should be
h = \frac{r}{2} \cos \theta
above A for the skier to lose contact at A.
If \theta=0 one gets h = r/2 = 18\, {\rm m}, which is the solution given by the book.
The problem in my opinion is that h is a decreasing function of \theta. This means that the height for losing contact at an angle \theta>0 is less than 18\, {\rm m}. This in turn means that if the first hill is 18\, {\rm m} above the second, the skier will definitely lose contact before reaching the crest of the second hill.
So, if I'm correct, the proposed exercise is not very hard, and in a way it's nice, but it does not make a lot of sense.
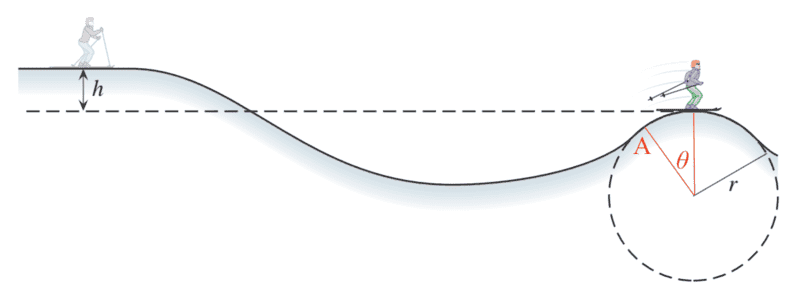
The figure is below. I added point A and angle \theta.
The solution is pretty easy. For the purpose of my discussion I'm assuming that the height is zero at the "center" of the rightmost hill, and consider a generic point A on such hill, instead of its crest. The radius going through A forms an angle \theta with the vertical direction. The answer to the question can be obtained by setting \theta =0 in the solution.
The condition for losing contact at A is that the normal force there is null, which means that the centrifugal force equals the projection of the weight along the radial direction. This gives v^2 = g r \cos \theta.
Conservation of total mechanical energy requires that 2 g h_0 =2 g r \cos \theta + v^2, where h_0 is the height of the leftmost hill wrt the center of the leftmost hill. Substituting the first equation into the second one we get
h_0 = \frac{3}{2} r \cos \theta
Since the height of point A is r \cos \theta, the starting point should be
h = \frac{r}{2} \cos \theta
above A for the skier to lose contact at A.
If \theta=0 one gets h = r/2 = 18\, {\rm m}, which is the solution given by the book.
The problem in my opinion is that h is a decreasing function of \theta. This means that the height for losing contact at an angle \theta>0 is less than 18\, {\rm m}. This in turn means that if the first hill is 18\, {\rm m} above the second, the skier will definitely lose contact before reaching the crest of the second hill.
So, if I'm correct, the proposed exercise is not very hard, and in a way it's nice, but it does not make a lot of sense.
Last edited: