Apogee
- 45
- 1
Momentum conservation is an immediate corollary of Newton's Laws. If we define a system such that no net external force acts on it, then:
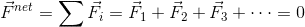
By Newton's Second Law, force is equal to the product of mass and acceleration. Since mass is constant, integrating over force gives us the product of mass and the integral of acceleration, or velocity. This product is defined to be momentum and intuitively is the quantity of force through time required to bring an object from rest to a certain velocity (or equivalently from a certain velocity back to rest). Therefore:
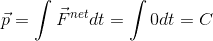
The total momentum of the system remains conserved. As one can see, this is a direct result of Newton's Second Law.
Energy conservation is entirely different. In theory, it could technically still hold without Newton's Laws, or equivalently with different definitions of forces. Energy conservation is more of a mathematical construct grounded in line integrals and the notion of work.
First, we shall define energy as work through some force vector field. The scalar work W done on an object by a force along some directional vector is given by:
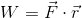
By letting r become small and summing all increments of work along a path, work can be defined along nonlinear paths by:
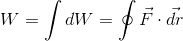
A conservative force is defined as any force for which this line integral is independent of the path taken. A good example of this is the electric force. The electric force can be defined by the charge of the object acted upon and the electric field magnitude, analogous to Newton's Second Law. The electric field is defined as the gradient of electric potential, literally potential energy per unit charge. Therefore:
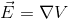
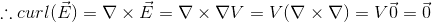
Thus, the electric field is a conservative vector field:
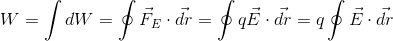
Because the line integral is independent of path, the product of the charge and the line integral is no different, for the curl of the vector field in either case still equals 0.
The purpose of this example is to illustrate that energy conservation is more of a mathematical construct and acts independently of the definition of force itself, rather depends on the nature of the particular force in question. Momentum conservation on the other hand relies entirely on Newton's Second Law, the way that we've commonly defined forces. If we redefined force to be the product of the mass and jerk instead of mass and acceleration, assuming we kept the definition for momentum, momentum conservation would no longer hold, but energy would still be conserved in systems undergoing conservative forces alone. Energy conservation only does not hold when nonconservative forces are at play.
By Newton's Second Law, force is equal to the product of mass and acceleration. Since mass is constant, integrating over force gives us the product of mass and the integral of acceleration, or velocity. This product is defined to be momentum and intuitively is the quantity of force through time required to bring an object from rest to a certain velocity (or equivalently from a certain velocity back to rest). Therefore:
The total momentum of the system remains conserved. As one can see, this is a direct result of Newton's Second Law.
Energy conservation is entirely different. In theory, it could technically still hold without Newton's Laws, or equivalently with different definitions of forces. Energy conservation is more of a mathematical construct grounded in line integrals and the notion of work.
First, we shall define energy as work through some force vector field. The scalar work W done on an object by a force along some directional vector is given by:
By letting r become small and summing all increments of work along a path, work can be defined along nonlinear paths by:
A conservative force is defined as any force for which this line integral is independent of the path taken. A good example of this is the electric force. The electric force can be defined by the charge of the object acted upon and the electric field magnitude, analogous to Newton's Second Law. The electric field is defined as the gradient of electric potential, literally potential energy per unit charge. Therefore:
Thus, the electric field is a conservative vector field:
Because the line integral is independent of path, the product of the charge and the line integral is no different, for the curl of the vector field in either case still equals 0.
The purpose of this example is to illustrate that energy conservation is more of a mathematical construct and acts independently of the definition of force itself, rather depends on the nature of the particular force in question. Momentum conservation on the other hand relies entirely on Newton's Second Law, the way that we've commonly defined forces. If we redefined force to be the product of the mass and jerk instead of mass and acceleration, assuming we kept the definition for momentum, momentum conservation would no longer hold, but energy would still be conserved in systems undergoing conservative forces alone. Energy conservation only does not hold when nonconservative forces are at play.