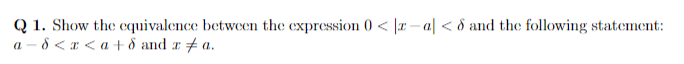Homework Help Overview
The discussion revolves around understanding the equivalence of inequalities involving absolute values, specifically the expression ##0 < |x - a| < \delta##. Participants are exploring the foundational properties of inequalities and absolute values in a mathematical context.
Discussion Character
- Exploratory, Conceptual clarification, Assumption checking
Approaches and Questions Raised
- Participants discuss the initial steps when dealing with absolute values, suggesting the consideration of cases based on the sign of the expression. There is mention of sketching a number line to visualize the problem. Questions arise regarding the properties of inequalities and the implications of multiplying by positive or negative numbers.
Discussion Status
Some participants have provided guidance on how to approach the problem, emphasizing the importance of showing work and understanding the properties of inequalities. There is an acknowledgment of gaps in mathematical background, which may affect comprehension. The discussion is ongoing, with participants reflecting on their understanding.
Contextual Notes
Participants note the challenges posed by their mathematical background and the cumulative nature of learning in mathematics, suggesting that earlier material may need to be reviewed for better understanding.