Graduate Initial value ODE with shifting forcing function

[Houeto]

Use laplace Transform to solve this ode:

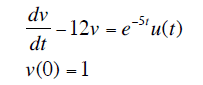
So I got:

sV(s)-V(0)-12V(s)=U(s+5)
V(s)(s-12)=U(s+5)+1
V(s)=[U(s+5)+1]/(s-12)

Now to go back to time domain with Inverse Laplace Transform...My question is, how to transform U(s+5)/(s-12)?

Any help?

Thanks guys

 

[Twigg]

I think it may help you to know that u(t) is the standard symbol for the step function, which has a known Laplace transform. Check your tables.

 

[Houeto]

Thanks

 

[Houeto]

@Twigg , can you shed some lights on Laplace Transform of e^(at)*u(t)?

Thanks

 

[Twigg]

I'm pretty sure you just apply the shifting property to the Laplace transform of the Heaviside step function. The Laplace transform of $u(t)$ is $\frac{1}{s}$, so the Laplace transform of $e^{-5t} u(t)$ is $\frac{1}{s + 5}$. Just like you did in your first post.

 

[Houeto]

Thanks