- #1
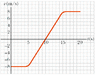
Instananeous accerlerations on a velocity vs time graph
In summary: If not, you can see it by clicking on your user name and then clicking on "view conversation".In summary, the problem asks for the instantaneous accelerations at 2.0 s, 10 s, and 18 s. The formula for acceleration is a= lim (change in x) / (change in y) as t->0. The first two values are given as 0 m/s2, and the third value can be found by selecting a point before or after when v != 0 on the velocity vs. time graph.
- #2
Doc Al
Mentor
- 45,569
- 2,219
Hint: Another way to express this is to say that acceleration is the slope of the velocity vs time graph.mandy9008 said:
- #3
Axiom17
- 70
- 0
As Doc Al said, a good way to go about understanding this question is to simply think of the slope of the velocty vs. time graph as representing the acceleration. So the greater the gradient of the slope, i.e. the steaper the line, then the greater the acceleration at that time.
OK so you've got the graph plotted of what's going on, that's good. It's much easier to visualise what's going on and know if you're right when able to look at a graph.
This is stating, rather more confusingly than it could be, that as has been said already that the acceleration is equal to the change in x, i.e. the change in the velocity, with respect to the change in y, i.e. the change in time. Hopefully that's clearer now if it wasn't already.
OK so you've got the first 2 correct, not sure if that was through applying the formula, a bit of guesswork, or just intuition. They're simple once you understand what's going on here.
For the acceleration at [itex]10.0s[/itex], just apply the formula, using the value for the velocity at this time that can be read off the graph.
Hope that helps now
OK so you've got the graph plotted of what's going on, that's good. It's much easier to visualise what's going on and know if you're right when able to look at a graph.
This is stating, rather more confusingly than it could be, that as has been said already that the acceleration is equal to the change in x, i.e. the change in the velocity, with respect to the change in y, i.e. the change in time. Hopefully that's clearer now if it wasn't already.
OK so you've got the first 2 correct, not sure if that was through applying the formula, a bit of guesswork, or just intuition. They're simple once you understand what's going on here.
For the acceleration at [itex]10.0s[/itex], just apply the formula, using the value for the velocity at this time that can be read off the graph.
Hope that helps now
- #4
Axiom17
- 70
- 0
Apologies just realized that method won't work very well I guess I'm not too with it at the moment!
Because the gradient of the line doesn't change around the time [itex]10.0s[/itex] what you can do is pick a point just before or after when [itex]v \neq 0[/itex] and thus you can get a non-zero value for the velocity and an accompanying time, then can find the acceleration using that simple formula.
I guess I'm not too with it at the moment! Because the gradient of the line doesn't change around the time [itex]10.0s[/itex] what you can do is pick a point just before or after when [itex]v \neq 0[/itex] and thus you can get a non-zero value for the velocity and an accompanying time, then can find the acceleration using that simple formula.
- #5
inky
- 99
- 1
mandy9008 said:
I wonder I don't know who delete my calculation .
- #6
Axiom17
- 70
- 0
inky said:
.. pardon?!
- #7
- 12,175
- 182
Your calculation was deleted because you are not supposed to do the calculation. The student who asked the question is supposed to do the calculation.inky said:
Did you not see the message I sent you?
1. What is instantaneous acceleration?
Instantaneous acceleration is the rate of change of velocity at a specific moment in time. It is a measure of how quickly an object's velocity is changing, and in what direction.
2. How is instantaneous acceleration represented on a velocity vs time graph?
Instantaneous acceleration is represented by the slope of the tangent line on a velocity vs time graph. The steeper the slope, the greater the instantaneous acceleration.
3. How is instantaneous acceleration calculated from a velocity vs time graph?
Instantaneous acceleration can be calculated by finding the slope of the tangent line at a specific point on a velocity vs time graph. This can be done using the formula a = Δv/Δt, where Δv is the change in velocity and Δt is the change in time.
4. What does a positive instantaneous acceleration indicate on a velocity vs time graph?
A positive instantaneous acceleration indicates that the object is speeding up, or increasing its velocity. This can be seen as an upward slope on the graph.
5. What does a negative instantaneous acceleration indicate on a velocity vs time graph?
A negative instantaneous acceleration indicates that the object is slowing down, or decreasing its velocity. This can be seen as a downward slope on the graph.
Similar threads
-
Introductory Physics Homework Help
-
Introductory Physics Homework Help
-
Introductory Physics Homework Help
-
Introductory Physics Homework Help
-
Introductory Physics Homework Help
-
Introductory Physics Homework Help
-
Introductory Physics Homework Help
-
Introductory Physics Homework Help
-
Introductory Physics Homework Help
-
Introductory Physics Homework Help