Interference in 2D (wavefronts)

[~ak~]

Homework Statement

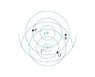
The figure shows the circular wave fronts emitted by two wave sources.


Make a table with rows labeled P, Q, and R and columns labeled r₁, r₂, \Deltar, and C/D. Fill in the table for points P, Q, and R, giving the distances as multiples of \lambda and indicating, with a C or a D, whether the interference at that point is constructive or destructive

Homework Equations

no real formula, given, just count the rings in the wave front pattern

The Attempt at a Solution

so i got mostly everything except r2 for P and R...im thinking it should be 7/2\lambda for both, but apparently its not...what am i doing wrong?

 

[Redbelly98]

Welcome to Physics forums.

Is the distance from "2" to the smallest ring equal to λ or λ/2?

What did you get for r2 and Q, that was verified as correct?

 

[~ak~]

thanks a lot redbelly...i can't believe i missed that, but i do have another question regarding this question. I can see that the 2 sources are out of phase but the only explanation that I can give is that 2 in-phase sources emit circular or spherical waves and these 2 dont. Is that correct?

 

[Redbelly98]

Not quite, out-of-phase point sources emit circular or spherical waves as well. It's just a matter of accounting for that phase difference when figuring out where there's constructive or destructive interference.