Interference of rectangular pulse

[sapiental]

Question Details:
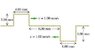
The figure shows two rectangular wave pulses
traveling toward each other on a stretched string.
Each pulse is traveling with a speed of 1.00 mm/s,
and has the height and width shown in the figure.
If the leading edges of the pulses are 8.00 mm
apart at t = 0, sketch the shape of the string at
t = 4.00 s, t = 6.00 s, and t = 10.0

you guys don't have to sketch the result for me but please be as descriptive as possible.

Im thinking that at t = 4s the 2 pulses will meet. If the pulses were of equal amplitude the string would be at equilibrium. But the right one is 4.00mm so I think it will look something like a upward pulse with 1.00mm amplitude and 4.00mm width?

At t = 6s the pulses will be 4mm apart. One pulse traveling in the negative x direction with an amplitude of 4mm and width 4mm and velocity 1mm/s. The second pulse traveling in the positive x direction with amplitude 3mm, width 4mm, and velocity 1mm.

not sure about t = 10s, but i think the problem wants us to presume that the pulses reflect off the wall..

Any help is much appreciated. And could you guys also explain how you got your answers.. i.e. by what rules etc. tho one I can think of is the principle of superposition (y(x,t) = y1(x,t) + y2(x,t). thanks

Please see the attached pic for the diagram.

 

[berkeman]

You have the right idea -- just add them with superposition. Where is the wall you are referring to?

 

[kyle8921]

I would first like to clarify the parameters of the problem. It states that the pulses are traveling with a speed of 1.00 mm/s, but does not specify the direction of this velocity. I will assume that both pulses are traveling in opposite directions, as shown in the diagram.

At t = 4.00 s, the two pulses will meet at the point where the distance between their leading edges is 4.00 mm. The resulting shape of the string at this time can be described by the principle of superposition, which states that the total displacement of a medium at a given point and time is equal to the sum of the displacements caused by each individual wave. In this case, the two pulses will interfere with each other, resulting in a new wave with a higher amplitude.

Since the right pulse has an amplitude of 4.00 mm and the left pulse has an amplitude of 3.00 mm, the resulting wave will have an amplitude of 7.00 mm. The width of the new wave will be equal to the sum of the widths of the two original pulses, which is 8.00 mm. Therefore, at t = 4.00 s, the string will have a new pulse with an amplitude of 7.00 mm, a width of 8.00 mm, and a velocity of 1.00 mm/s in the direction of the right pulse.

At t = 6.00 s, the two pulses will have moved further apart and will be 4.00 mm apart. The left pulse will have traveled a distance of 6.00 mm, while the right pulse will have traveled a distance of 2.00 mm. The resulting shape of the string at this time can be described by the principle of superposition again. The left pulse will now have an amplitude of 2.00 mm, a width of 4.00 mm, and a velocity of 1.00 mm/s in the negative x direction. The right pulse will still have an amplitude of 4.00 mm, a width of 4.00 mm, and a velocity of 1.00 mm/s in the positive x direction.

At t = 10.00 s, the two pulses will have reached the end of the string and will be reflected back in the opposite direction. They will continue to interfere with each other as they travel back towards each other. The resulting shape of the