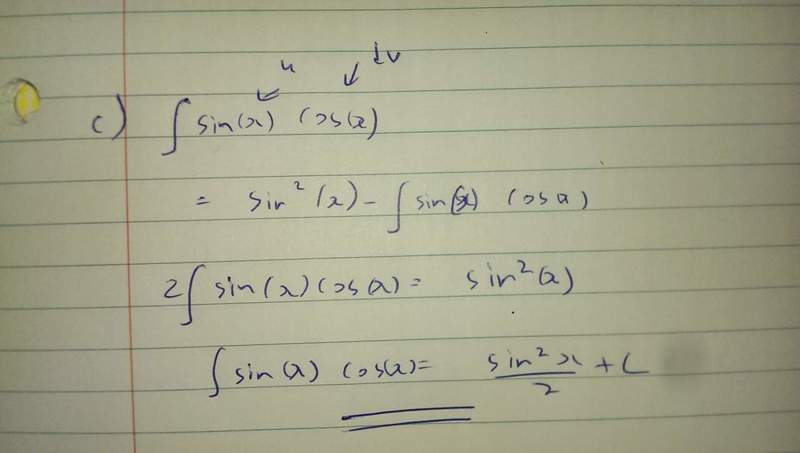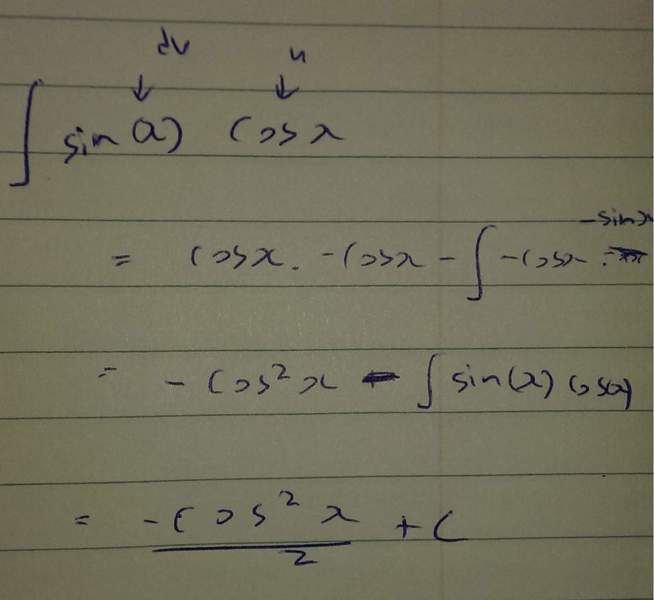SUMMARY
The forum discussion centers on the integration of sin(x)cos(x) using the integration by parts method, specifically the LIATE method. The user explores the implications of choosing u=cos(x) and dv=sin(x), leading to different forms of the integral. The discussion highlights that multiple correct answers can arise from different methods, such as substitution and trigonometric identities, ultimately differing only by a constant. This reinforces the concept that various integration techniques yield equivalent results.
PREREQUISITES
- Understanding of integration techniques, specifically integration by parts.
- Familiarity with the LIATE method for selecting u and dv.
- Knowledge of trigonometric identities, particularly sin(2x) = 2sin(x)cos(x).
- Basic concepts of antiderivatives and the reverse power rule.
NEXT STEPS
- Study the LIATE method in detail for effective integration by parts.
- Learn about trigonometric substitutions and their applications in integration.
- Explore the concept of equivalence in integrals and how constants affect results.
- Practice integrating functions using both substitution and integration by parts to compare outcomes.
USEFUL FOR
Students and educators in calculus, mathematicians exploring integration techniques, and anyone seeking to deepen their understanding of trigonometric integrals and their equivalences.