Internal angle sum of triangle

[bonfire09]

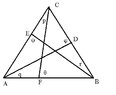
Problem: Let A, B, C be three non-collinear points. Let D, E, F be points on the respective interiors of segments BC, AC and AB. Let θ, φ and ψ be the measures of the respective angles ∠BFC, ∠CDA and ∠AEB. Prove IAS(ABC) < θ +φ + ψ < 540 - IAS(ABC).(IAS means internal angle sum). Now I am supposed to use the external angle inequality which is the measure of an exterior angle of a triangle is greater than that of either opposite interior angle. Not sure how to do it. I've been struggling for hours with it. Oh i forgot to mention this is still in absolute geometry so we can't use that the the angles of a triangle add up to 180*.

 

[BAdhi]

consider the following triangles,

$\Delta ABE$,
$$\psi =180-\left[{A}+({B}-r)\right]\qquad (1)$$
$\Delta ADC$,
$$\varphi = 180-\left[{C}+({A}-q)\right]\qquad (2)$$
$\Delta ABE$,
$$\theta = 180-\left[{B}+({C}-p)\right]\qquad (3)$$

Adding (1),(2),(3) together,

$$\psi+\varphi+\theta=540-(A+B+C)-\underbrace{[(A-q)+(B-r)+(C-p)]}_{>0}$$
you can derive one inequality from this

then,
from $\Delta ABD$
$$B+q=\varphi \qquad (4)$$
from $\Delta AFC$
$$A+p=\theta\qquad (5)$$
from $\Delta BCE$
$$C+r=\psi\qquad (6)$$

adding (4),(5),(6) together,
$$(A+B+C)+\underbrace{(p+q+r)}_{>0}=\varphi+\theta+\psi$$

from this you can get the other inequiality