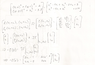Robb
- 225
- 8
Homework Statement
Homework Equations
The Attempt at a Solution
My initial thought was to set the two equations equal to each other but the resulting equation is linear which gives a constant for a Newton iteration. I thought about Taylor's theorem in 2-d but I'm not so sure about that as far as deriving the iterating function. Please help!