zenterix
- 774
- 84
- Homework Statement
- A positively charged ion with charge ##q## and mass ##m##, initially at rest inside the source, is accelerated across a gap by an electric potential difference with magnitude ##\Delta v## . The ion enters a region of uniform magnetic field ##B_1## pointing into the page of the figure below and follows a semi-circular trajectory of radius ##R_1##. The ion is again accelerated across the gap, increasing its speed, by an electric potential difference that has the opposite sign but has the same magnitude ##|\Delta v|##. The ion then enters a region of uniform magnetic field ##B_2## pointing into the page of the figure below and follows a semi-circular trajectory of radius ##R_2##.
- Relevant Equations
- a) What is the ratio ##B_2/B_1##?
b) What is the ratio ##v_2/v_1##?
My question is about item (b).
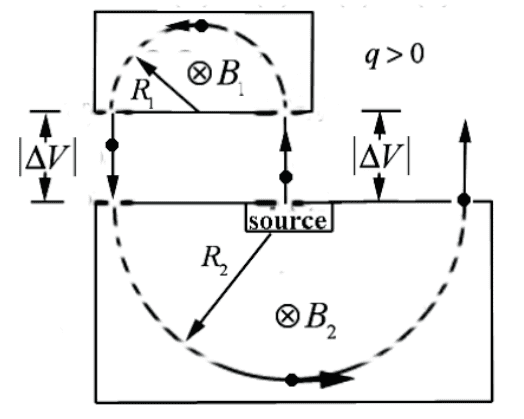
For item (a) we have uniform circular motion in the regions with uniform magnetic field.
$$\vec{F}_{B_1}=qv\hat{\theta}_1\times B_1(-\hat{k})=-qv_1B_1\hat{r}_1=-mR_1\theta'^2\hat{r}_1\tag{1}$$
$$B_1=\frac{mv_1}{R_1q}\tag{2}$$
A similar calculation for the bottom portion of the trajectory gives
$$B_2=\frac{mv_2}{R_2q}\tag{3}$$
Thus,
$$\frac{B_2}{B_1}=\frac{R_1v_2}{R_2v_1}\tag{4}$$
As for item (b), I don't understand the following.
The problem statement says that the ion is accelerated in both of the gaps. It also says that the electric potential difference in the gap on the left is the negative of the electric potential difference of the gap on the right.
How then can a positively charged ion accelerate across both gaps?
Let's assume that the potential at the "source" is higher than on the top part of the gap above it.
$$q\Delta v=-W=-\Delta K_e=-\frac{mv_1^2}{2}\tag{5}$$
$$v_1=\sqrt{-\frac{2q}\Delta V}{m}}\tag{6}$$
Note that ##\Delta v<0##.
Now consider the gap on the left side.
The speed of the ion is the same ##v_1## when it enters the gap, but now it is traversing from a lower to a higher potential as a positive charge. Shouldn't it slow down (to zero speed)?
For item (a) we have uniform circular motion in the regions with uniform magnetic field.
$$\vec{F}_{B_1}=qv\hat{\theta}_1\times B_1(-\hat{k})=-qv_1B_1\hat{r}_1=-mR_1\theta'^2\hat{r}_1\tag{1}$$
$$B_1=\frac{mv_1}{R_1q}\tag{2}$$
A similar calculation for the bottom portion of the trajectory gives
$$B_2=\frac{mv_2}{R_2q}\tag{3}$$
Thus,
$$\frac{B_2}{B_1}=\frac{R_1v_2}{R_2v_1}\tag{4}$$
As for item (b), I don't understand the following.
The problem statement says that the ion is accelerated in both of the gaps. It also says that the electric potential difference in the gap on the left is the negative of the electric potential difference of the gap on the right.
How then can a positively charged ion accelerate across both gaps?
Let's assume that the potential at the "source" is higher than on the top part of the gap above it.
$$q\Delta v=-W=-\Delta K_e=-\frac{mv_1^2}{2}\tag{5}$$
$$v_1=\sqrt{-\frac{2q}\Delta V}{m}}\tag{6}$$
Note that ##\Delta v<0##.
Now consider the gap on the left side.
The speed of the ion is the same ##v_1## when it enters the gap, but now it is traversing from a lower to a higher potential as a positive charge. Shouldn't it slow down (to zero speed)?